ЬтФПФкШн
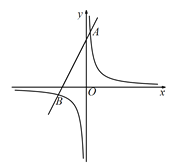
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЁЂ
ЁЂ![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() жсЗелЕУЕН
жсЗелЕУЕН![]() ЃЌвбжЊХзЮяЯп
ЃЌвбжЊХзЮяЯп![]() Й§Еу
Й§Еу![]() ЁЂ
ЁЂ![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
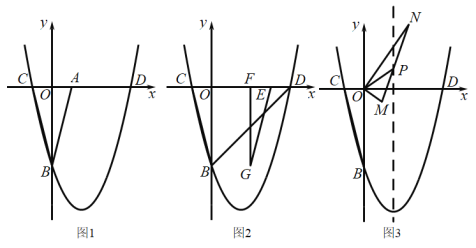
ЃЈ1ЃЉХзЮяЯпЖЅЕуЕФзјБъЮЊ_______ЃЛ
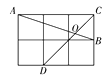
ЃЈ2ЃЉШчЭМ2ЃЌ![]() би
би![]() жсЯђгввдУПУы
жсЯђгввдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЦНвЦЕУЕН
ИіЕЅЮЛГЄЖШЕФЫйЖШЦНвЦЕУЕН![]() ЃЌдЫЖЏЪБМфЮЊ
ЃЌдЫЖЏЪБМфЮЊ![]() УыЃЎЕБ
УыЃЎЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() гы
гы![]() жиЕўУцЛ§
жиЕўУцЛ§![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
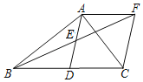
ЃЈ3ЃЉШчЭМ3ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊЕУЕН
ЫГЪБеыа§зЊЕУЕН![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() гыХзЮяЯпЖдГЦжсНЛгкЕу
гыХзЮяЯпЖдГЦжсНЛгкЕу![]() ЃЎдка§зЊвЛШІЙ§ГЬжаЃЌЪЧЗёДцдкЕу
ЃЎдка§зЊвЛШІЙ§ГЬжаЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃПШєДцдкЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФЕу
ЃПШєДцдкЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЪдЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЪдЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉДцдкЃЌЃЈ
ЃЛЃЈ3ЃЉДцдкЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩжсЖдГЦПЩЕУЕуBЁЂCзјБъЃЌПЩЧѓЕУХзЮяЯпНтЮіЪНЃЌНјЖјЕУЕНХзЮяЯпЖЅЕузјБъЃЛ
ЃЈ2ЃЉИљОнЬтвтЙЙдьЯрЫЦШ§НЧаЮЃЌгУtБэЪОЖдгкЯпЖЮЃЌдйгУИюВЙЗЈБэЪО![]() гы
гы![]() жиЕўУцЛ§МДПЩЃЛ
жиЕўУцЛ§МДПЩЃЛ
ЃЈ3ЃЉгЩЬтвтПЩжЊЃЌЕуPЮЊЯпЖЮMNжаЕуЃЌгЩХзЮяЯпаджЪЃЌЧѓЕУPЕузјБъЃЌЩшГіMЃЈmЃЌnЃЉзјБъЃЌдйгЩШ§НЧаЮЯрЫЦПЩЕУNЕузјБъЃЌгУжаЕузјБъЙЋЪНПЩБэЪОPЕузјБъЃЌЙЙдьЗНГЬПЩЧѓmЃЌnЃЌдђЮЪЬтПЩНт.
НтЃКЃЈ1ЃЉгЩвбжЊЃЌЕуCзјБъЮЊЃЈ-1,0ЃЉ
АбЃЈ-1,0ЃЉЃЌЃЈ0ЃЌ-4ЃЉДњШы![]() ЃЌЕУ
ЃЌЕУ
![]()
НтЕУЃЌ![]()
Ёр![]()
дђЖдГЦжсЮЊжБЯп![]()
ЖЅЕузнзјБъЮЊЃК![]()
Ёр ЖЅЕузјБъЮЊ![]()
ЙЪД№АИЮЊЃК![]()
ЃЈ2ЃЉСЌBGЃЌЩшBDНЛGEгкЕуKЃЌBDНЛFGгк TЃЌЙ§KзіHKЁЭFGгкH

гЩЃЈ1ЃЉПЩжЊЃЌЕуDзјБъЮЊЃЈ4,0ЃЉ
дђ![]()
гЩвбжЊЃЌ![]() ЃЌ
ЃЌ
ЁпGBЁЮOD
Ёр![]()
дђга![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЕУЃК![]()
![]() ЃЌ
ЃЌ
![]()
![]()
ЃЈ3ЃЉЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ШчЭМЃЌЕБMдкЕкЫФЯѓЯоЪБЃЌИљОнЬтвтПЩжЊЃКЕБЕу![]() ЪЧ
ЪЧ![]() жаЕуЪБЃЌ
жаЕуЪБЃЌ![]()
ЁрMN=BC=![]()
дђ![]() ЃЌ
ЃЌ
PЕНxжсОрРыЮЊЃК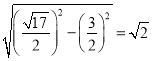
ПЩЕУЃК![]()
ЗжБ№Й§ЕуMЁЂNзїMFЁЭyжсгкЕуFЃЌNEЁЭyжсгкЕуE
![]()
0
Ёп![]()
Ёр![]()
Ёп![]()
Ёр![]()
![]()
ЁрЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЁрЕуPзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
Ёр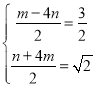
НтЕУ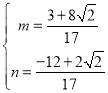
ЁрMзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЕБЕуMдкЕкШ§ЯѓЯоЪБЃЌЭЌРэЃЌЩш![]() ЃЌдђ
ЃЌдђ![]()
ЁрЕуPзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЭЌРэЕу![]()
Ёр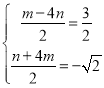
НтЕУ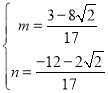
ЁрMзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЙЪД№АИЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ

 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ