Question

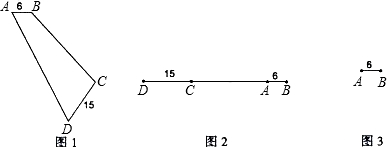
如图1，四根长度一定的木条，其中AB=6cm，CD=15cm，将这四根木条用小钉绞合在一起，构成一个四边形ABCD（在A、B、C、D四点处是可以活动的）．现固定AB边不动，转动这个四边形，使它的形状改变，在转动的过程中有以下两个特殊位置．
位置一：当点D在BA的延长线上时，点C在线段AD上（如图2）；
位置二：当点C在AB的延长线上时，∠C=90°．
（1）在图2中，若设BC的长为x，请用x的代数式表示AD的长；
（2）在图3中画出位置二的准确图形；（各木条长度需符合题目要求）
（3）利用图2、图3求图1的四边形ABCD中，BC、AD边的长．

Answer 1

（1）∵在四边形ABCD的转动过程中，BC、AD边的长度始终保持不变，BC=x，
∴在图2中，AC=BC-AB=x-6，AD=AC+CD=x+9．

（2）∴位置二的图见图3．

（3）∵在四边形ABCD转动的过程中，BC、AD边的长度始终保持不变，
∴在图3中，BC=x，AC=AB+BC=6+x，AD=x+9，
∵图3中，△ACD为直角三角形，∠C=90°，
由勾股定理得：AC²+CD²=AD²，
∴（6+x）²+15²=（x+9）²
整理，得6x=180，
解得x=30
即BC=30，
∴AD=39．