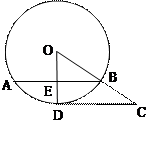
题目内容
如图,CD切⊙O于点D,连接OC,交⊙O于点B,过点B作弦AB∥DC,点E为垂足,已知⊙O的半径为6,
(1)若OE=4,求弦AB的长;
(2)若DC=6
,求劣弧AB的长.

(1)若OE=4,求弦AB的长;
(2)若DC=6
| 3 |
分析:(1)由CD为圆O的切线,根据切线的性质得到CD与OD垂直,又AB与DC平行,根据与平行线中的一条直线垂直,与另一条也垂直可得OE与AB垂直,根据垂径定理可得E为AB的中点,即AB=2EB,在直角三角形OEB中,由OE及OB的长,利用勾股定理求出EB的长,可得出AB的长;
(2)由DC与OD垂直,可得三角形ODC为直角三角形,在直角三角形ODC中,由DC及OD的长,利用锐角三角函数定义表示出∠COD的正切值,利用特殊角的三角函数值求出∠COD的度数,然后利用弧长公式求出弧BD的长,又OE与AB垂直,根据垂径定理得到D为劣弧AB的中点,可得出弧AB的长等于弧BD长的2倍.
(2)由DC与OD垂直,可得三角形ODC为直角三角形,在直角三角形ODC中,由DC及OD的长,利用锐角三角函数定义表示出∠COD的正切值,利用特殊角的三角函数值求出∠COD的度数,然后利用弧长公式求出弧BD的长,又OE与AB垂直,根据垂径定理得到D为劣弧AB的中点,可得出弧AB的长等于弧BD长的2倍.
解答:解:(1)∵CD为圆O的切线,
∴CD⊥OD,
∴∠ODC=90°,又AB∥DC,
∴∠OEB=∠ODC=90°,
在Rt△OEB中,OE=4,OB=6,
根据勾股定理得:EB=
=2
,
又OE⊥AB,
∴E为弦AB的中点,
则AB=2BE=4
;
(2)由∠ODC=90°,得到△OCD为直角三角形,
∵DC=6
,OD=6,
∴tan∠COD=
=
=
,
∴∠COD=60°,
又OE⊥AB,
∴D为
的中点,即
=
=
=2π,
则
=2
=4π.
∴CD⊥OD,
∴∠ODC=90°,又AB∥DC,
∴∠OEB=∠ODC=90°,
在Rt△OEB中,OE=4,OB=6,
根据勾股定理得:EB=
| OB2-OE2 |
| 5 |
又OE⊥AB,
∴E为弦AB的中点,
则AB=2BE=4
| 5 |
(2)由∠ODC=90°,得到△OCD为直角三角形,
∵DC=6
| 3 |
∴tan∠COD=
| CD |
| OD |
6
| ||
| 6 |
| 3 |
∴∠COD=60°,
又OE⊥AB,
∴D为
 |
| AB |
 |
| AD |
 |
| BD |
| 60π×6 |
| 180 |
则
 |
| AB |
 |
| BD |
点评:此题考查了切线的性质,平行线的性质,垂径定理,勾股定理,锐角三角函数,以及弧长公式,熟练掌握定理及性质是解本题的关键.

练习册系列答案
相关题目
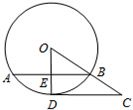 10,sin∠COD=
10,sin∠COD= 如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为15,sin∠COD=
如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为15,sin∠COD=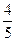 .
.