题目内容
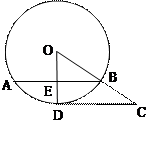
如图,CD切⊙O于点D,连接OC,交⊙O于点B,过点B作弦,点E为垂足,已知⊙O的半径为10,s in∠COD=
in∠COD=| 4 | 5 |
(1)求弦AB的长;
(2)CD的长;
(3)劣弧AB的长(结果保留三个有效数字,sin53.13°≈0.8,π≈3.142).
分析:(1)利用sin∠COD=
=
,已知OB=10,所以BE=8,所以AB=16;
(2)根据题意可知△OBE∽△OCD,根据相似三角形的比求CD的长;
(3)解直角三角形求出弧所对的圆心角,然后利用弧长公式计算.
| 4 |
| 5 |
| BE |
| OB |
(2)根据题意可知△OBE∽△OCD,根据相似三角形的比求CD的长;
(3)解直角三角形求出弧所对的圆心角,然后利用弧长公式计算.
解答:解:(1)∵AB⊥OD,
∴∠OEB=90°
在Rt△OEB中,BE=OB×sin∠COD=10×
=8
由垂径定理得AB=2BE=16
所以弦AB的长是16;(2分)
(2)方法(一)
在Rt△OEB中,OE=
=
=6.
∵CD切⊙O于点D,
∴∠ODC=90°,
∴∠OEB=∠ODC.
∵∠BOE=∠COD,
∴△BOE∽△COD,
∴
=
,
∴
=
,
∴CD=
.
所以CD的长是
.(3分)
方法(二)由sin∠COD=
可得tan∠COD=
,
在Rt△ODC中,tan∠COD=
,
∴CD=OD•tan∠COD=10×
=
;(3分)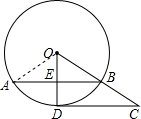
(3)连接OA,
在Rt△ODC中,
∵sin53.13°≈0.8
∴∠DOC=53.13°,
∴∠AOB=106.26°,
∴劣弧AB的长度l=
=
≈18.5.(3分)
∴∠OEB=90°
在Rt△OEB中,BE=OB×sin∠COD=10×
| 4 |
| 5 |
由垂径定理得AB=2BE=16
所以弦AB的长是16;(2分)
(2)方法(一)
在Rt△OEB中,OE=
| OB2-BE2 |
| 102-82 |
∵CD切⊙O于点D,
∴∠ODC=90°,
∴∠OEB=∠ODC.
∵∠BOE=∠COD,
∴△BOE∽△COD,
∴
| CD |
| BE |
| OD |
| OE |
∴
| CD |
| 8 |
| 10 |
| 6 |
∴CD=
| 40 |
| 3 |
所以CD的长是
| 40 |
| 3 |
方法(二)由sin∠COD=
| 4 |
| 5 |
| 4 |
| 3 |
在Rt△ODC中,tan∠COD=
| CD |
| OD |
∴CD=OD•tan∠COD=10×
| 4 |
| 3 |
| 40 |
| 3 |

(3)连接OA,
在Rt△ODC中,
∵sin53.13°≈0.8
∴∠DOC=53.13°,
∴∠AOB=106.26°,
∴劣弧AB的长度l=
| nπR |
| 180 |
| 106.26×3.142×10 |
| 180 |
点评:本题综合考查了解直角三角形和圆的有关知识,学生做数学题时一定要注意把各知识系统起来,才能提高做题能力.

练习册系列答案
相关题目
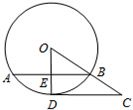 10,sin∠COD=
10,sin∠COD= 如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为15,sin∠COD=
如图,CD切⊙O于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为15,sin∠COD=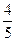 .
.