题目内容

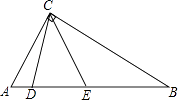
【题目】如图，在△ABC中，将△ABC在平面内绕点A逆时针旋转50角后得到△AB′C′的位置，若此时恰有CC′∥AB，则∠CAB′的度数为（ ）

A.15°
B.40°
C.50°
D.65°

【答案】A
【解析】∵△ABC绕点A旋转得到△AB′C′，
∴AC=AC′，∠CA C′=∠BAB′=50°
∴∠ACC′= (180°-50°)=65°，
∵CC′∥AB，
∴∠ACC′=∠BAC=65°．
∴∠CAB′=∠BAC-∠BAB′=65°-50°=15°.
故答案为：A．
据两直线平行，内错角相等可得∠ACC′=∠CAB，根据旋转的性质可得AC=AC′，然后利用等腰三角形两底角相等求∠CAC′，再根据∠CAC′、∠BAB′都是旋转角解答．

练习册系列答案
相关题目

【题目】小数在数学外小组活动中遇到这样一个问题：如果α、β都为锐角，且tanα= ，tanβ= ．求α+β的度数．

（1）小敏是这样解决问题的：如图1，把α，β放在正方形网格中，使得∠ABD=α，∠CBE=β，且BA，BC在直线BD的两侧，连接AC，可证得△ABC是等腰直角三角形，因此可求得α+β=∠ABC=°．
（2）请你参考小敏思考问题的方法解决问题：如果α，β都为锐角，当tanα=4，tanβ= 时，在图2的正方形网格中，利用已作出的锐角α，画出∠MON=α﹣β，由此可得α﹣β=°．

【题目】某商场为了吸引顾客，设立了一可以自由转动的转盘，AB为转盘直径，如图所示，并规定：顾客消费100元（含100元）以上，就能获得一次转盘的机会，如果转盘停止后，指针正好对准9折、8折、7折区域，顾客就可以获得相应的优惠．

（1）某顾客正好消费99元，是否可以获得相应的优惠．

（2）某顾客正好消费120元，他转一次转盘获得三种打折优惠的概率分别是多少？

【题目】规定两数a，b之间的一种运算，记作(a，b)：如果，那么(a，b)=c．

例如：因为23=8，所以(2，8)=3．

（1）根据上述规定，填空：

（3，27）=_______，（5，1）=_______，（2，）=_______．

（2）小明在研究这种运算时发现一个现象：（3n，4n）=（3，4）小明给出了如下的证明：

设（3n，4n）=x，则（3n）x=4n，即（3x）n=4n

所以3x=4，即（3，4）=x，

所以（3n，4n）=（3，4）．

请你尝试运用这种方法证明下面这个等式：(3，4)+(3，5)=(3，20)

【题目】如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为（度）．

【题目】如图①所示，已知，BC∥OA，∠B=∠A=100°，试解答下列问题：

（1）试说明：OB∥AC；

（2）如图②，若点E．F在BC上，且∠FOC=∠AOC，OE平分∠BOF.试求∠EOC的度数；

（3）在（2）小题的条件下，若左右平行移动AC，如图③，那么∠OCB：∠OFB的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值.

（4）在（3）小题的条件下，当∠OEB=∠OCA时，试求∠OCA的度数.

【题目】如图所示，三角形ABC（记作△ABC）在方格中，方格纸中的每个小方格都是边长为1个单位的正方形，三个顶点的坐标分别是A（﹣2，1），B（﹣3，﹣2），C（1，﹣2），先将△ABC向上平移3个单位长度，再向右平移2个单位长度，得到A1B1C1．

（1）在图中画出△A1B1C1；

（2）点A1，B1，C1的坐标分别为　 　、　 　、　 　；

（3）若y轴有一点P，使△PBC与△ABC面积相等，求出P点的坐标．

【题目】如图，从①∠1＝∠2；②∠C＝∠D；③∠A＝∠F三个条件中选出两个作为已知条件，另一个作为结论所组成的命题中，正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3

【题目】如图，△ABC中，AD是BC边上的中线，E，F为直线AD上的点，连接BE，CF，且BE∥CF．

（1）求证：DE＝DF；

（2）若在原有条件基础上再添加AB＝AC，你还能得出什么结论．（不用证明）（写2个）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网