题目内容
【题目】小数在数学外小组活动中遇到这样一个问题:如果α、β都为锐角,且tanα= ![]() ,tanβ=
,tanβ= ![]() .求α+β的度数.
.求α+β的度数.
(1)小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得α+β=∠ABC=°.
(2)请你参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ= ![]() 时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β,由此可得α﹣β=°.
时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β,由此可得α﹣β=°.
【答案】
(1)45
(2)45
【解析】解:如图1,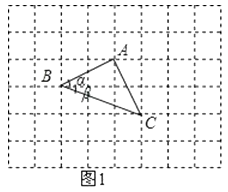
把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰三角形,
因此可求得α+β=∠ABC=45°;
参考小敏思考问题的方法解决问题:
如果α,β都为锐角,当tanα=4,tanβ= ![]() 时,在图2
时,在图2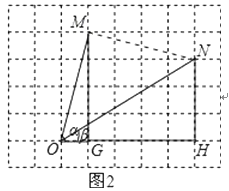
的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β,由此可得α﹣β=45°.
所以答案是:45;45.
【考点精析】掌握等腰直角三角形和正方形的性质是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目



