题目内容
阅读下列材料:
∵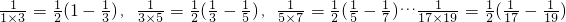
∴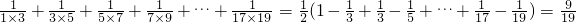
解答问题:
(1)在式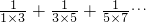 中,第六项为______,第n项为______,上述求和的想法是通过逆用______法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以______从而达到求和的目的;
中,第六项为______,第n项为______,上述求和的想法是通过逆用______法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以______从而达到求和的目的;
(2)解方程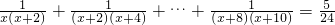 .
.
解:根据以上分析(1) ;
;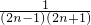 ;分式的加减法,相互抵消.
;分式的加减法,相互抵消.
(2)化简得; -
-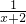 +
+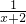 -
-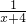 +…+
+…+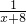 -
- =
=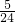 ,
, ×(
×( -
- )=
)=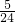
方程两边都乘24x(x+10),得
12(x+10)-12x=5x(x+10)
解得x=-12或x=2
经检验x=-12和x=2为原方程的解.
分析:(1)分子都是1,分母的两个因式里是两个相邻的奇数.
(2)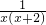 =
= ×(
×( -
-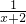 )后面的式子依此类推,使得除首末两项外的中间各项可以相互抵消从而达到求和的目的.
)后面的式子依此类推,使得除首末两项外的中间各项可以相互抵消从而达到求和的目的.
点评:解决本题的关键是理解题意,找到规律进而简化式子,注意解分式方程需要验根.
 ;
;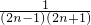 ;分式的加减法,相互抵消.
;分式的加减法,相互抵消.(2)化简得;
 -
-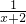 +
+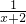 -
-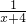 +…+
+…+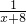 -
- =
=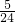 ,
, ×(
×( -
- )=
)=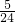
方程两边都乘24x(x+10),得
12(x+10)-12x=5x(x+10)
解得x=-12或x=2
经检验x=-12和x=2为原方程的解.
分析:(1)分子都是1,分母的两个因式里是两个相邻的奇数.
(2)
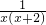 =
= ×(
×( -
-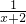 )后面的式子依此类推,使得除首末两项外的中间各项可以相互抵消从而达到求和的目的.
)后面的式子依此类推,使得除首末两项外的中间各项可以相互抵消从而达到求和的目的.点评:解决本题的关键是理解题意,找到规律进而简化式子,注意解分式方程需要验根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
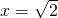 ;当y2=4时,x2-1=4,∴
;当y2=4时,x2-1=4,∴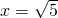 .
.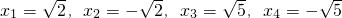 .
.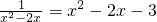 ,如果设x2-2x=y,那么原方程可化为________(写成关于y的一元二次方程的一般形式).
,如果设x2-2x=y,那么原方程可化为________(写成关于y的一元二次方程的一般形式).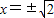 ;当y2=4时,x2-1=4,∴
;当y2=4时,x2-1=4,∴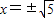 .
.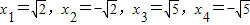 .
.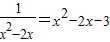 ,如果设x2-2x=y,那么原方程可化为______(写成关于y的一元二次方程的一般形式).
,如果设x2-2x=y,那么原方程可化为______(写成关于y的一元二次方程的一般形式).