题目内容
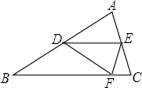
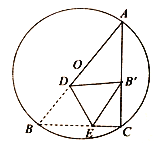
【题目】如图,![]() 内接于
内接于![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的两个动点(不与端点
上的两个动点(不与端点![]() 、
、![]() 、
、![]() 重合),将
重合),将![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点
的对应点![]() 恰好落在线段
恰好落在线段![]() 上(包含端点
上(包含端点![]() 、
、![]() ),若
),若![]() 为等腰三角形,则
为等腰三角形,则![]() 的长为__.
的长为__.
【答案】![]() 或
或![]() 或
或![]()
【解析】
分三种情况讨论:当AB'=DB'时,△ADB′是等腰三角形;当AD=AB'时,△ADB′是等腰三角形;当AD=B'D时,△AEB′是等腰三角形,分别根据等腰三角形的性质以及勾股定理进行计算,即可得到CB′的值.
解:![]() 内接于
内接于![]() ,
,![]() 为
为![]() 的直径,
的直径,
∴∠C=90°,
∵BC=3,AB=5,
∴AC=4,
分三种情况讨论:
①如图所示,当AD=DB'时,△ADB′是等腰三角形;

∴DB=B'D=AD,
即:D点与O点重合,B'与C重合,
AD=![]()
②如图所示,当B'D=AB'时,△AEB′是等腰三角形,
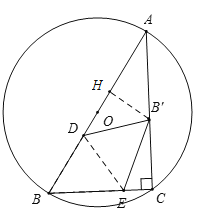
过B'作B'H⊥AB,垂足为H,
∴AH=DH
∴△AHB'∽△ABC
设AB'=B'D=BD=5x,则AH= DH =4x,HB'=3x,
∴AB=BD+DH+AH=13x,
即13x=5,x=![]() ,
,
AD=8x=![]()
③如图所示,当AD=AB'时,△AEB′是等腰三角形,
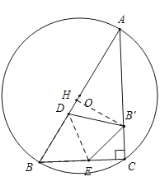
过B'作B'H⊥AB,垂足为H,
∴△AHB'∽△ABC
设AB'=AD=5x,则AH=4x,HB'=3x,DH=x,
∴DB=DB'=![]() =
=![]() =
=![]()
∴5x+![]() =5
=5
解得![]() ,
,
∴AD=5x=![]() .
.
综上所述:AD的长为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目