题目内容
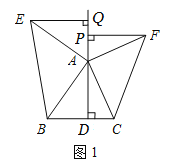
【题目】如图①,ΔABC中,AD⊥BC于点D,以A为直角顶点,分别以AB、AC为直角边,向ΔABC外作等腰RtΔABE和等腰RtΔACF,过点E、F作射线DA的垂线,垂足分别为Q、P.
(1)试探究线段EQ和FP之间的数量关系,并说明理由.
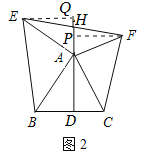
(2)如图②,若连接EF交DA的延长线于点H,由(1)中的结论你能判断EH与FH的大小关系吗?并说明理由.
(3)图②中的ΔABC与ΔAEF的面积相等吗?(直接给出结论,不需要说理)


【答案】(1)EQ=FP,理由见解析;(2)HE=HF,理由见解析;(3)相等,理由见解析.
【解析】
(1)根据AAS得出△EAQ≌△ABD,可得EQ=AD,同理AD=FP,由此可得结论;
(2)过点E作EQ⊥DA,过点F作FP⊥DA,垂足分别为Q、P.根据AAS证明△EQH≌△FPH即可;
(3)由(1)、(2)中的全等三角形可以推得△ABC与△AEF的面积相等.
解:(1)EQ=FP,理由如下:
如图1,∵Rt△ABE是等腰三角形,∴EA=BA.
∵∠QEA+∠QAE=90°,∠QAE+∠BAD=90°,
∴∠QEA=∠BAD.
在△EAQ与△ABD中,
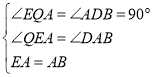 ,
,
∴△EAQ≌△ABD(AAS),
∴EQ=AD.
同理AD=FP.
∴EQ=FP.
(2)HE=HF,理由如下:
如图2,过点E作EQ⊥DA,过点F作FP⊥DA,垂足分别为Q、P.
由(1)知EQ=FP.
在△EQH与△FPH中,
∵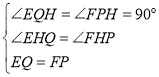 ,
,
∴△EQH≌△FPH(AAS).
∴HE=HF;
(3)相等.理由如下:
由(1)知,△ABD≌△EAQ,△FPA≌△ADC,则S△ABD=S△EAQ,S△FPA=S△ADC.
由(2)知,△EQH≌△FPH,则S△EQH=S△FPH,
所以S△ABC=S△ABD+S△ADC=S△EAQ﹣S△EQH+S△FPA﹣S△FPH=S△EAH+S△FHA=S△AEF,即S△ABC=S△AEF.
故图②中的△ABC与△AEF的面积相等.







