Question

【题目】如图，△ABC是等边三角形，BC＝2.点P从点A出发沿沿射线AB以1的速度运动，过点P作PE∥BC交射线AC于点E，同时点Q从点C出发沿BC的延长线以1的速度运动，连结BE、EQ.设点P的运动时间为t（）.

（1）求证：△APE是等边三角形；

（2）直接写出CE的长（用含的代数式表示）；

（3）当点P在边AB上，且不与点A、B重合时，求证：△BPE≌△ECQ.

（4）在不添加字母和连结其它线段的条件下，当图中等腰三角形的个数大于3时，直接写出t的值和对应的等腰三角形的个数.

Answer 1

【答案】（1）见解析；（2）2-t或t-2；（3）见解析；（4）当t=1时，图中有5个等腰三角形；当t=4时，图中有4个等腰三角形

【解析】

（1）根据等边三角形的性质可得∠A=∠ABC=∠ACB =60°，根据平行线的性质可得∠APE=∠ABC=60°，∠AEP=∠ACB=60°，再利用等边三角形的判定即可得证；

（2）由（1）可得AE=AP=t，分E没过C点与过C点两种情况进行解答即可；

（3）△ABC与△APE都是是等边三角形，利用等边三角形的性质易证BP=EC，∠BPE=∠ECQ=120°，再通过“边角边”证明△BPE≌△ECQ即可；

（4）当P在AB的中点，即t=1时，图中有5个等腰三角形；当P点在AP=2AB，即t=4时，图中有4个等腰三角形.

（1）∵△ABC是等边三角形，

∴∠A=∠ABC=∠ACB =60°，

∵，

∴∠APE=∠ABC=60°，∠AEP=∠ACB=60°．

∴△APE是等边三角形；

（2）∵△APE是等边三角形，

∴AE=AP=t，

当E点没过C点时，AE=2﹣t；

当E点过了C点时，AE=t﹣2；

（3）∵△ABC是等边三角形，

∴AB=AC，∠ACB=60°．

∵△APE是等边三角形，

∴AP=PE=AE，∠APE=60°．

∴AB-AP=AC-AE，∠BPE=∠ECQ=120°，

∴BP=EC，

∵AP=CQ=t，

∴PE=CQ，

∴△BPE≌ECQ（SAS）；

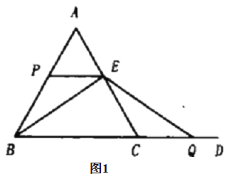
（4）如图1，当t=1时，图中有5个等腰三角形：△ABC，△APE，△PBE，△CQE，△EBQ；

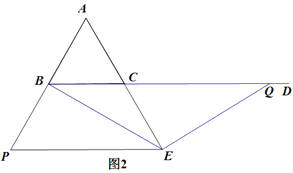
如图2，当t=4时，图中有4个等腰三角形:△ABC，△APE，△CBE，△EQB.