Question

【题目】如图1，正方形ABCD中，点E是BC延长线上一点，连接DE，过点B作BF⊥DE于点F，连接FC

．

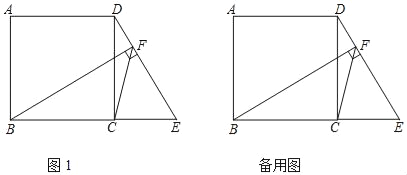
（1）求证：∠FBC=∠CDF．

（2）作点C关于直线DE的对称点G，连接CG，FG．

①依据题意补全图形；

②用等式表示线段DF，BF，CG之间的数量关系并加以证明．

Answer 1

【答案】(1)见解析;(2) ①见解析；②BF=DF+CG，理由见解析.

【解析】分析：（1）由∠FBC+∠COB=90°，∠CDF+∠DOF=90°，根据等角的余角相等证明即可；

（2）①根据题意画出图形即可；②结论：BF=DF+CG．利用截长补短法，构造相似三角形解决问题即可；

详解：（1）证明：如图1中，设CD交BF于点O．

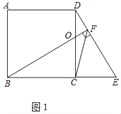
∵四边形ABCD是正方形，

∴∠BCO=90°，

∵BF⊥DE，

∴∠OFD=∠OCB=90°，

∴∠FBC+∠COB=90°，∠CDF+∠DOF=90°，

∵∠DOF=∠BOC，

∴∠FBC=∠CDF．

（2）解：①如图2中，

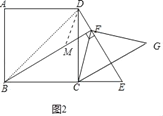
②结论：BF=DF+CG．

理由：在线段FB上截取FM，使得FM=FD．

∵∠BDC=∠MDF=45°，

∴∠BDM=∠CDF，

∵==，

∴△BDM∽△CDF，

∴==，∠DBM=∠DCF，

∴BM=CF，

∴∠CFE=∠FCD+∠CDF=∠DBM+∠BDM=∠DMF=45°，

∴∠EFG=∠EFC=45°，

∴∠CFG=90°，

∵CF=FG，

∴CG=CF，

∴BM=CG，

∴BF=BM+FM=CG+DF．