题目内容
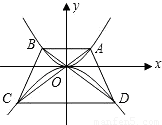
如图,点A在抛物线y=| 1 |
| 4 |
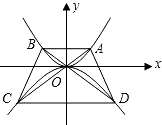 抛物线y=-
抛物线y=-| 1 |
| 8 |
(1)当m=1时,求点A,B,D的坐标;
(2)当m为何值时,四边形ABCD的两条对角线互相垂直;
(3)猜想线段AB与CD之间的数量关系,并证明你的结论.
分析:(1)根据题意得点A的坐标是将x=1代入即可,根据对称性可得点B的坐标,即可得OB的解析式,与二次函数的解析式组成方程组即可求得点D的坐标;
(2)当四边形ABCD的两对角线互相垂直时,由对称性得直线AO与x轴的夹角等于45°所以点A的纵、横坐标相等,根据点A在二次函数y=
x2上,即可求得m的值;
(3)根据题意求得点A,B的坐标,求得AC的长与BD的解析式,即可求得点D与C的坐标,求得CD的长,可得CD=2AB.
(2)当四边形ABCD的两对角线互相垂直时,由对称性得直线AO与x轴的夹角等于45°所以点A的纵、横坐标相等,根据点A在二次函数y=
| 1 |
| 4 |
(3)根据题意求得点A,B的坐标,求得AC的长与BD的解析式,即可求得点D与C的坐标,求得CD的长,可得CD=2AB.
解答:解:(1)∵点A在抛物线y=
x2上,且x=m=1,
∴A(1,
),(1分)
∵点B与点A关于y轴对称,
∴B(-1,
).(2分)
设直线BD的解析式为y=kx,
∴k=-
,
∴y=-
x.(3分)
解方程组
,
得D(2,-
).(4分)
(2)当四边形ABCD的两对角线互相垂直时,
由对称性得直线AO与x轴的夹角等于45°
所以点A的纵、横坐标相等,(5分)
这时,
设A(a,a),代入y=
x2,
得a=4,
∴A(4,4),
∴m=4.
即当m=4时,四边形ABCD的两条对角线互相垂直.(7分)
(3)线段CD=2AB.(8分)
证明:∵点A在抛物线y=
x2,且x=m,
∴A(m,
m2),
得直线AO的解析式为y=
x,
解方程组
,
得点C(-2m,-
m2)(9分)
由对称性得点B(-m,
m2),D(2m,-
m2),(10分)
∴AB=2m,CD=4m,
∴CD=2AB.(11分)
| 1 |
| 4 |
∴A(1,
| 1 |
| 4 |
∵点B与点A关于y轴对称,
∴B(-1,
| 1 |
| 4 |
设直线BD的解析式为y=kx,
∴k=-
| 1 |
| 4 |
∴y=-
| 1 |
| 4 |
解方程组
|
得D(2,-
| 1 |
| 2 |
(2)当四边形ABCD的两对角线互相垂直时,
由对称性得直线AO与x轴的夹角等于45°
所以点A的纵、横坐标相等,(5分)
这时,
设A(a,a),代入y=
| 1 |
| 4 |
得a=4,
∴A(4,4),
∴m=4.
即当m=4时,四边形ABCD的两条对角线互相垂直.(7分)
(3)线段CD=2AB.(8分)
证明:∵点A在抛物线y=
| 1 |
| 4 |
∴A(m,
| 1 |
| 4 |
得直线AO的解析式为y=
| m |
| 4 |
解方程组
|
得点C(-2m,-
| 1 |
| 2 |
由对称性得点B(-m,
| 1 |
| 4 |
| 1 |
| 2 |
∴AB=2m,CD=4m,
∴CD=2AB.(11分)
点评:此题考查了二次函数与一次函数的综合知识,要注意对称性质的应用,要注意数形结合思想的应用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,点P在抛物线y=x2-4x+3上运动,若以P为圆心,2为半径的⊙P在x轴上截得的弦长为
如图,点P在抛物线y=x2-4x+3上运动,若以P为圆心,2为半径的⊙P在x轴上截得的弦长为 如图,点P在抛物线y=x2-3x+1上运动,若以P为圆心的圆与x轴、y轴都相切,则符合上述条件的所有的点P共有( )
如图,点P在抛物线y=x2-3x+1上运动,若以P为圆心的圆与x轴、y轴都相切,则符合上述条件的所有的点P共有( ) x2上,过点A作与x轴平行的直线交抛物线于点B,延长AO,BO分别与抛物线y=-
x2上,过点A作与x轴平行的直线交抛物线于点B,延长AO,BO分别与抛物线y=- x2相交于点C,D,连接AD,BC,设点A的横坐标为m,且m>0.
x2相交于点C,D,连接AD,BC,设点A的横坐标为m,且m>0.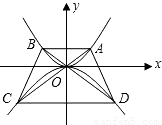
 x2上,过点A作与x轴平行的直线交抛物线于点B,延长AO,BO分别与抛物线y=-
x2上,过点A作与x轴平行的直线交抛物线于点B,延长AO,BO分别与抛物线y=- x2相交于点C,D,连接AD,BC,设点A的横坐标为m,且m>0.
x2相交于点C,D,连接AD,BC,设点A的横坐标为m,且m>0.