题目内容
 如图,点P在抛物线y=x2-4x+3上运动,若以P为圆心,2为半径的⊙P在x轴上截得的弦长为2
如图,点P在抛物线y=x2-4x+3上运动,若以P为圆心,2为半径的⊙P在x轴上截得的弦长为2| 3 |
(2-
,1)或(2+
,1)或(2,-1)
| 2 |
| 2 |
(2-
,1)或(2+
,1)或(2,-1)
.| 2 |
| 2 |
分析:根据⊙P的半径为2,以及⊙P与x轴相交且截得的弦为2
,即可得出y=1,求出x的值即可得出答案.
| 3 |
解答: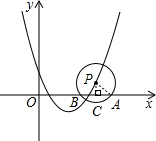 解:∵⊙P的半径为2,圆心P在抛物线y=x2-4x+3上运动,
解:∵⊙P的半径为2,圆心P在抛物线y=x2-4x+3上运动,
∴当⊙P与x轴相交时,假设交点为AB,
∵在x轴上截得的弦长为2
,
∴AB=2
,
如图,作PC⊥x轴于点C,
∴AC=
AB=
,
由勾股定理得PC=1,
∴|x2-4x+3|=1,
∴x2-4x+3=1或x2-4x+3=-1
解得:x=2±
或x=2
∴P点的坐标为:(2-
,1)或(2+
,1)或(2,-1)
故答案为:(2-
,1)或(2+
,1)或(2,-1).
 解:∵⊙P的半径为2,圆心P在抛物线y=x2-4x+3上运动,
解:∵⊙P的半径为2,圆心P在抛物线y=x2-4x+3上运动,∴当⊙P与x轴相交时,假设交点为AB,
∵在x轴上截得的弦长为2
| 3 |
∴AB=2
| 3 |
如图,作PC⊥x轴于点C,
∴AC=
| 1 |
| 2 |
| 3 |
由勾股定理得PC=1,
∴|x2-4x+3|=1,
∴x2-4x+3=1或x2-4x+3=-1
解得:x=2±
| 2 |
∴P点的坐标为:(2-
| 2 |
| 2 |
故答案为:(2-
| 2 |
| 2 |
点评:此题主要考查了图象上点的性质以及切线的性质,根据题意得出y=1,求出x的值是解决问题的关键.

练习册系列答案
相关题目
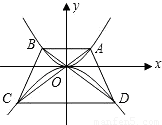
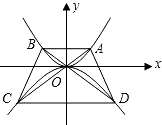 抛物线y=-
抛物线y=- 如图,点P在抛物线y=x2-3x+1上运动,若以P为圆心的圆与x轴、y轴都相切,则符合上述条件的所有的点P共有( )
如图,点P在抛物线y=x2-3x+1上运动,若以P为圆心的圆与x轴、y轴都相切,则符合上述条件的所有的点P共有( ) x2上,过点A作与x轴平行的直线交抛物线于点B,延长AO,BO分别与抛物线y=-
x2上,过点A作与x轴平行的直线交抛物线于点B,延长AO,BO分别与抛物线y=- x2相交于点C,D,连接AD,BC,设点A的横坐标为m,且m>0.
x2相交于点C,D,连接AD,BC,设点A的横坐标为m,且m>0.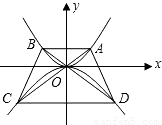
 x2上,过点A作与x轴平行的直线交抛物线于点B,延长AO,BO分别与抛物线y=-
x2上,过点A作与x轴平行的直线交抛物线于点B,延长AO,BO分别与抛物线y=- x2相交于点C,D,连接AD,BC,设点A的横坐标为m,且m>0.
x2相交于点C,D,连接AD,BC,设点A的横坐标为m,且m>0.