题目内容
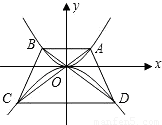
如图，点P在抛物线y=x2-3x+1上运动，若以P为圆心的圆与x轴、y轴都相切，则符合上述条件的所有的点P共有（ ）分析：若以P为圆心的圆与x轴、y轴都相切，则点P的横纵坐标的绝对值相等，即x=±y，再判定一元二次方程是否有解即可．
解答：解：∵若以P为圆心的圆与x轴、y轴都相切，
∴x=y或x=-y，
当x=y时，即x2-3x+1=x，
∵△=b2-4ac=12＞0，
∴方程有两个不相等的实数解；
当x=-y时，即x2-3x+1=-x，
∵△=b2-4ac=0，
∴方程有两个相等的实数解；
综上可知符合上述条件的所有的点P共有3个，
故选B．
∴x=y或x=-y，
当x=y时，即x2-3x+1=x，
∵△=b2-4ac=12＞0，
∴方程有两个不相等的实数解；
当x=-y时，即x2-3x+1=-x，
∵△=b2-4ac=0，
∴方程有两个相等的实数解；
综上可知符合上述条件的所有的点P共有3个，
故选B．
点评：此题主要考查了图象上点的性质以及切线的性质，根据题意得出x=±y，求出x的值是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
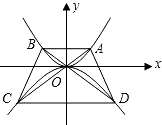抛物线y=-
如图，点P在抛物线y=x2-4x+3上运动，若以P为圆心，2为半径的⊙P在x轴上截得的弦长为
x2上，过点A作与x轴平行的直线交抛物线于点B，延长AO，BO分别与抛物线y=-
x2相交于点C，D，连接AD，BC，设点A的横坐标为m，且m＞0．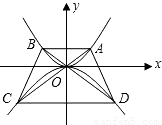
x2上，过点A作与x轴平行的直线交抛物线于点B，延长AO，BO分别与抛物线y=-
x2相交于点C，D，连接AD，BC，设点A的横坐标为m，且m＞0．