题目内容
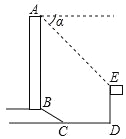
【题目】如图,一边靠墙,其他三边用12米长的篱笆围成一个矩形(ABCD)花圃.

(1)如果设花圃靠墙的一边的长为x(米).花圃的面积为y(平方米),求x,y满足的关系式;
(2)当长x从4米变到6米时,面积y变化如何?
(3)当长x从6米变到8米时,面积y变化如何?
【答案】(1)![]() ;(2)面积y由16变为18;(3)面积y由18变为16
;(2)面积y由16变为18;(3)面积y由18变为16
【解析】
(1)AD=x,则AB=![]() ,根据矩形面积=长×宽,即可得出y与x的函数关系式;
,根据矩形面积=长×宽,即可得出y与x的函数关系式;
(2)将x=4,x=6代入(1)中的关系式可得y的变化;
(3)将x=6,x=8代入(1)中的关系式可得y的变化.
解:(1)由题得AD=x,∵ABCD为矩形,
∴AD=BC,CD=AB,
又∵AB+BC+CD=12,
∴AB=![]() ,
,
则y=![]()
![]() =
=![]() ,
,
故答案为:y=![]() ;
;
(2)∵x=4时,代入(1)中关系式y=16,
x=6时,代入(1)中关系式y=18,
∴当长x从4米变到6米时,面积y由16变为18;
(3)∵x=6时,代入(1)中关系式y=18,
x=8时,代入(1)中关系式y=16,
∴当长x从6米变到8米时,面积y由18变为16;

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
螺丝 | a | 1.0 | 2.0 |
螺母 | a﹣0.3 | 0.6 | 2.0 |
(1)已知用50元购进螺丝的数量与用20元购进螺母的数量相同,求表中a的值;
(2)若该店购进螺母数量是螺丝数量的3倍还多200个,且两种配件的总量不超过3000个.
①该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:怎样进货,才能获得最大利润?最大利润是多少?(用含a的代数式表示)
②由于原材料价格上涨,每个螺丝和螺母的进价都上涨了0.1元.按照①中的最佳进货方案,在销售价不变的情况下,全部售出后,所得利润比①少了260元,请问本次成套的销售量为多少?

【题目】小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,到校后,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
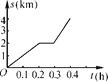
时间t/h | 0 | 0.2 | 0.3 | 0.4 |
路程s/km |
(3)路程s可以看成时间t的函数吗?