题目内容
作图题(不写作法,保留作图痕迹)
(1)已知正方形ABCD,求作点P,使点P是边AB的黄金分割点,且AP>PB;
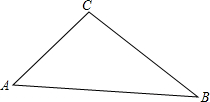
(2)已知△ABC,在线段BC上求作一点P,连接AP,使得S△ABP:S△ACP=3:2.
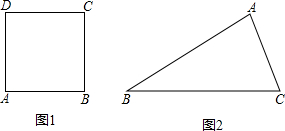
(1)已知正方形ABCD,求作点P,使点P是边AB的黄金分割点,且AP>PB;
(2)已知△ABC,在线段BC上求作一点P,连接AP,使得S△ABP:S△ACP=3:2.

分析:(1)在BC是取点D′使BE=
AB,连接AD′,在AD上截取D′E=D′B,在线段AB上截取AP=AE,则点P是线段AB的一个黄金分割点.
(2)由题意可知三角形ABP和三角形ACP为同高的三角形,所以面积比等于底之比,由此在线段BC上截取BP=
CP即可.
| 1 |
| 2 |
(2)由题意可知三角形ABP和三角形ACP为同高的三角形,所以面积比等于底之比,由此在线段BC上截取BP=
| 3 |
| 2 |
解答:解:(1)如图,点P是线段AB的一个黄金分割点.(2)如图所示:点P为所求
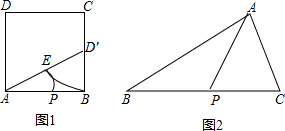
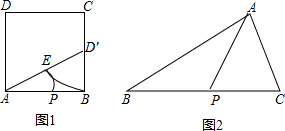
点评:(1)本考查了黄金分割点的概念.特别注意这里的AP可能是较长线段,也可能是较短线段;熟记黄金比的值进行计算;
(2)本题考查了画线段等于已知线段的倍数,和三角形的面积公式,属于基础性题目.
(2)本题考查了画线段等于已知线段的倍数,和三角形的面积公式,属于基础性题目.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目

 作图题(不写作法,保留作图痕迹)
作图题(不写作法,保留作图痕迹)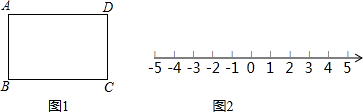
 作图题(不写作法,保留作图痕迹):
作图题(不写作法,保留作图痕迹):