Question

在四边形ABCD中，对角线AC，BD交于点O，点P是在线段BC上任意一点（与点B不重合），∠BPE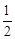＝∠BCA，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．

      

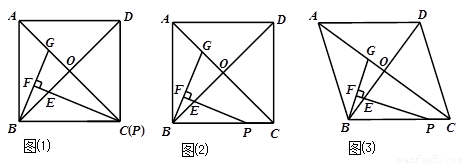
⑴ 若ABCD为正方形，

① 如图⑴，当点P与点C重合时．△BOG是否可由△POE通过某种图形变换得到？证明你的结论；

② 结合图⑵求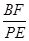的值；

⑵ 如图⑶，若ABCD为菱形，记∠BCA＝，请探究并直接写出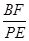的值．（用含的式子表示）

 

Answer 1

【答案】

（1）①△BOG可由△POE绕点O顺时针旋转90°得到

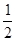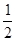②＝  （2）＝tanα

【解析】

试题分析：⑴ 解：△BOG可由△POE绕点O顺时针旋转90°得到．

 

证明：如图，∵四边形ABCD是正方形，P与C重合，

∴OB=OP，∠BOC=∠BOG=90°．

∵PF⊥BG，∠PFB=90°，

∴∠GBO=90°－∠BGO，

∠EPO=90°－∠BGO，

∴∠GBO=∠EPO，∴△BOG≌△POE．

∴OE=OG，

又∵∠EOG=90°，

∴将线段OE绕点O顺时针旋转90°就得到OG．

又∵OB=OP，∠POB=90°，

∴将线段OP绕点O顺时针旋转90°就得到OB．

∴△BOG可由△POE绕点O顺时针旋转90°得到．

⑵ 解法一：如图，作PM//AC交BG于M，交BO于N，

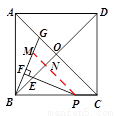
∴∠PNE=∠BOC=90°，∠BPN=∠OCB，

∵∠OBC=∠OCB=45°，∴∠NBP=∠NPB，

∴NB=NP．

∵∠MBN=90°－∠BMN， ∠NPE=90°－∠BMN，

∴∠MBN=∠NPE，

∴△BMN≌△PEN，

∴BM=PE．

∵∠BPE=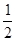∠ACB，∠BPN=∠ACB，

∴∠BPF=∠MPF．

∵PF⊥BM，∴∠BFP=∠MFP=90°．

又∵PF=PF， ∴△BPF≌△MPF，

∴BF="MF" ，即BF=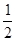BM，

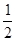∴BF=PE， 即＝．

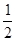解法二：如图，作CM//PF交BG于M，交BO于N，

∴，

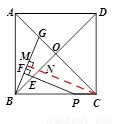
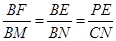且∠BPE=∠BCM，

∵∠BPE=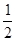∠ACB，

∴∠BCM=∠GCM，

∵CM//PF，PF⊥BG，∴CM⊥BG，

∴∠CMB=∠CMG=90°．

又∵CM=CM，∴△BCM≌△GCM，

∴BM=MG，即BM=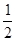BG，

又由⑴得，BG=CN．

∴．

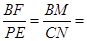
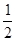⑶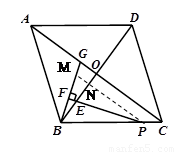

如图，过点P作PM∥AC，交BG于M，交BO于N

∴∠BAC=∠BPM=α,又∠BPE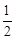＝∠BCA，

∴∠MPF=∠BPF,又∵PF⊥BG,PF=PF

∴△BPF≌△MPF

∴MF=BF

∵四边形ABCD是菱形，所以AC⊥BD

∵MP∥AC, ∴MP⊥BD

∴∠MNB=∠ENP

∵∠NEP=∠FEB

又∠FBE+∠FEB=90°=∠NPE+∠NEP

∴∠FBE=∠NPE

∴△BMN∽≌△PEN

∴

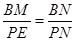
∵BM=2BF,在RT△BNP中，又∠BAC=∠BPM=α

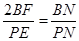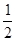∴=tanα

∴＝tanα

考点：菱形的性质、全等三角形、等腰三角形的性质、三角函数、图形变换

点评：几何综合题，中考压轴题种类， 难度系数较大，考查学生对几何综合知识的掌握程度和分析、解决问题的能力。