题目内容
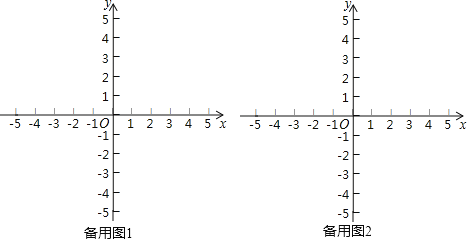
【题目】一座隧道的截面由抛物线和长方形的构成,长方形的长为8米,宽为2米,隧道的最高点P位于AB的中央且距地面6m.
(1)建立适当的直角坐标系,求抛物线解析式;
(2)如果隧道为单行道,一辆货车高4米,宽3米,能否从隧道内通过,说明理由.
【答案】(1) y=-![]() (x﹣4)2+6;(2)货车可以通过.
(x﹣4)2+6;(2)货车可以通过.
【解析】
(1)建立如图所示的坐标系,可得抛物线的顶点坐标(4,6),再利用待定系数法求函数的解析式即可;(2)令y=4,解方程求得x的值,计算|x1﹣x2|的值与3比较即可解答.
解:(1)由题意可知抛物线的顶点坐标(4,6),
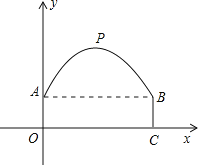
设抛物线的方程为y=a(x﹣4)2+6,
又∵点A(0,2)在抛物线上,
∴2=a(0-4)2+6,
∴a=-![]()
因此有:y=-![]() (x﹣4)2+6.
(x﹣4)2+6.
(2)令y=4,则有4=-![]() (x﹣4)2+6,
(x﹣4)2+6,
解得x1=4+2![]() ,x2=4﹣2
,x2=4﹣2![]() ,
,
|x1﹣x2|=4![]() >3,
>3,
故货车可以通过.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目