题目内容
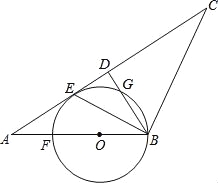
【题目】如图，在Rt△MNP中，∠N=60°，MN=3，NP=6，正方形ABCD的边长为1，它的一边AD在MN上，且顶点A与M重合．现将正方形ABCD沿边MN→NP进行翻滚，直到正方形有一个顶点与P重合即停止滚动，正方形在整个翻滚过程中，点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是（ ）
A．
+2 B．2π+2 C． D．
【答案】A.
【解析】
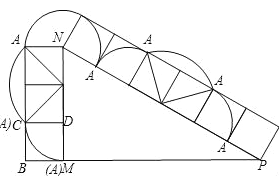
试题分析：第一次翻滚：绕D，点A围成的扇形是圆心角是90°，半径是1；第二次翻滚：绕C，点A围成的图形是扇形和两个三角形，扇形是圆心角是90°，半径是
，两个等腰直角三角形组成一个边长为1的正方形；第三次翻滚：绕B，点A围成的扇形是圆心角是210°，半径是1；第四次翻滚：绕A，点A不动；第五次翻滚：绕D，点A围成的扇形是圆心角是90°，半径是1；…依次重复，直到第八次翻滚结束．如图，点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积：
S=
×3+
×2+
+2=
×3+
×2+
+2=
+2．故选A.
练习册系列答案
相关题目
