题目内容
 如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,已知AB=8,大圆半径为5,则小圆半径为
如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,已知AB=8,大圆半径为5,则小圆半径为
- A.4.5
- B.4
- C.3
- D.2
C
分析:连接OA、OB、OP,OP即为小圆半径,易证△OAP≌△OBP,通过构建直角三角形,可解答.
解答: 解:连接OA、OB、OP,OP即为小圆半径,
解:连接OA、OB、OP,OP即为小圆半径,
∵OA=OB,∠OAB=∠OBA,∠OPA=∠OPB=90°,
∴△OAP≌△OBP,
∴在直角△OPA中,OA=5,AP=4,
∴OP=3.
故选C.
点评:本题主要考查了切线、勾股定理的应用,本题综合性较强;掌握其定理、性质,才能熟练解答.
分析:连接OA、OB、OP,OP即为小圆半径,易证△OAP≌△OBP,通过构建直角三角形,可解答.
解答:
 解:连接OA、OB、OP,OP即为小圆半径,
解:连接OA、OB、OP,OP即为小圆半径,∵OA=OB,∠OAB=∠OBA,∠OPA=∠OPB=90°,
∴△OAP≌△OBP,
∴在直角△OPA中,OA=5,AP=4,
∴OP=3.
故选C.
点评:本题主要考查了切线、勾股定理的应用,本题综合性较强;掌握其定理、性质,才能熟练解答.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
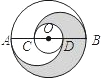 如图,在以O为圆心的两个同心圆中,大圆的直径AB交小圆于C、D两点,AC=CD=DB,分别以C、D为圆心,以CD为半径作圆.若AB=6cm,则图中阴影部分的面积为
如图,在以O为圆心的两个同心圆中,大圆的直径AB交小圆于C、D两点,AC=CD=DB,分别以C、D为圆心,以CD为半径作圆.若AB=6cm,则图中阴影部分的面积为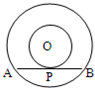 9、如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,已知AB=8,大圆半径为5,则小圆半径为( )
9、如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,已知AB=8,大圆半径为5,则小圆半径为( )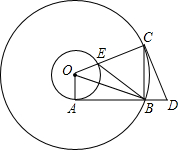 (2006•静安区二模)如图,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于B,大圆的弦BC⊥AB,过点C作大圆的切线交AB的延长线于D,OC交小圆于E
(2006•静安区二模)如图,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于B,大圆的弦BC⊥AB,过点C作大圆的切线交AB的延长线于D,OC交小圆于E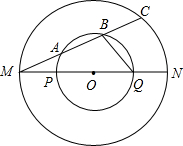 如图,在以O为圆心的两个同心圆中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP=1,MA=AB=BC,则△MBQ的面积为
如图,在以O为圆心的两个同心圆中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP=1,MA=AB=BC,则△MBQ的面积为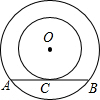 如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆的半径为5cm,小圆的半径为3cm,则弦AB的长为( )
如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆的半径为5cm,小圆的半径为3cm,则弦AB的长为( )