题目内容
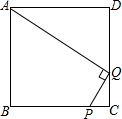 如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,若PQ⊥AQ,则CP=________.
如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,若PQ⊥AQ,则CP=________.

分析:证明△ADQ∽△QCP:已知的条件有∠C=∠D=90°,那么只要得出另外两组对应角相等即可得出两三角形相似,因为∠DQA+∠CQP=180°-90°=90°,而∠DAQ+∠DQA=90°,因此∠CQP=∠DAQ,那么就构成了两三角形相似的条件;然后由相似三角形的对应边成比例、正方形的四条边都相等及已知条件CQ=1,DQ=2求解即可.
解答:∵PQ⊥AQ,
∴∠DQA+∠CQP=180°-90°=90°;
又∵四边形ABCD是正方形,
∴∠DAQ+∠DQA=90°,
∴∠CQP=∠DAQ,
∴ADQ∽△QCP,
∴
 =
= ;
;∵CQ=1,DQ=2,
∴AD=DC=3;
∴CP=
 ;
;故答案:
 .
.点评:本题主要考查了正方形的性质、相似三角形的判定与性质.在求相似比时,一定要找对相似三角形的对应边.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
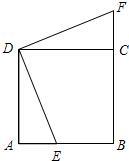 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以 向以
向以
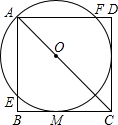 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.