题目内容
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.
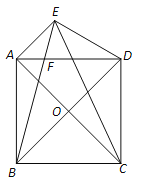
(1)求证:DE=DF;
(2)求证:AE∥BD;
(3)求tan∠ACE的值.
【答案】(1)证明见解析(2)证明见解析 (3)![]()
【解析】试题分析:(1)根据旋转的性质和等腰三角形的性质易得∠BDE=∠BED=75°,根据正方形的性质可得∠ADB=45°,所以∠EDF=30°,在△DEF中,根据三角形的内角和定理可得∠DFE=75°,所以∠DFE=∠DEF,即可得DE=DF ;(2)过点E作EG⊥BD于点G,易证四边形AOGE是矩形,即可得结论;(3)设EG=x,则BE=BD=AC=2EG=2x, Rt△BEG中,由勾股定理可得BG= ![]() ,即可得OG=(
,即可得OG=(![]() )x,再由AE=OG即可得结论.
)x,再由AE=OG即可得结论.
试题解析:
(1)∵BD绕点B逆时针旋转30°至BE,
∴∠DBE=30°,BD=BE,
∴∠BDE=∠BED=![]() =75°
=75°
在正方形ABCD中,BD是对角线,
∴∠ADB=45°,
∴∠EDF=75°-45°=30°,
在△DEF中,∠DFE=180°-∠EDF-∠FED
=180°-30°-75°
=75°
∴∠DFE=∠DEF
∴DE=DF
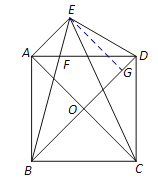
(2)证明:过点E作EG⊥BD于点G,
∵∠DBE=30°
∴EG= ![]()
在正方形ABCD中,AC、BD是对角线,
∴AC=BD,OA= ![]() ,AC⊥BD
,AC⊥BD
∴EG=OA且EG∥OA
∴四边形AOGE是平行四边形,
∴四边形AOGE是矩形
∴AE∥BD
(3)设EG=x,
则BE=BD=AC=2EG=2x,
Rt△BEG中,BG= ![]() ,
,
∴OG=BG-BO=(![]() )x,
)x,
在矩形AOGE中,∠EAO=90°
AE=OG=(![]() )x
)x
∴tan∠ACE=![]()

练习册系列答案
相关题目