题目内容
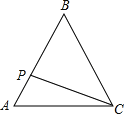
【题目】如图, ![]() 平分
平分![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)![]() .
.
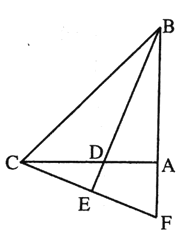
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)证明△ABD≌△ACF即可得到结论;
(2)由(1)得∠ABD=∠ACF,∠CDE=∠BDA,根据三角形内角和定理可得∠CED=∠BAD=90°,即BE⊥CF,结合BD平分∠ABC可证明BC=BF.
(1)∵∠BAC=90°,
∴∠CAF=90°,
∴∠BAC=∠CAF,
又∵AB=AC,AD=AF,
∴△ABD≌△ACF,
∴∠ABD=∠ACF;
(2)在△CDE和△BDA中
∵∠DEC+∠CDE+DCE=180°,∠ABD+∠BDA+∠BAD=180°
又∠ABD=∠ACF,∠CDE=∠BDA,
∴∠CED=∠BDA=90°,
∴∠CEB=∠FEB=90°,
∵BD平分∠ABC
∴∠CBE=∠FBE
又BE为公共边,
∴△CEB≌△FEB,
∴BC=BF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目