题目内容
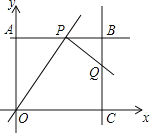
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
(1)求点B的坐标;
(2)当点P在线段AB上运动(不与A,B重合)时,设点P的横坐标为m,线段CQ的长度为l.求出l关于m的函数解析式;
(3)在坐标平面内是否存在点D,使以O、P、Q、D为顶点的四边形为正方形?若存在,请直接写出D点的坐标;若不存在,请说明理由.
【答案】(1)B(4,3);(2) ![]() ;(3)存在,D(3,-1)或(-3,7).
;(3)存在,D(3,-1)或(-3,7).
【解析】
(1)通过解方程求出线段的长度,利用矩形的性质得到AB=4,BC=3,求得B(4,3);
(2)因为点P在线段AB上,点P的横坐标为m,用m表示出AP的长度,利用相似三角形的性质列出比例式求出l关于m的函数解析式;
(3)如图,过点D作DE⊥OC于E,由以O、P、Q、D为顶点的四边形为正方形,得到OP=PQ=OD,通过三角形全等,对应边相等求得AP=m=1,再根据另一对三角形全等得到点D的坐标.
(1)解方程x2-7x+12=0得:x1=3,x2=4,
∴OA=3,OC=4,
∴A(0,3),C(4,0),
∵四边形OABC为矩形,
∴AB=4,BC=3,
∴B(4,3);
(2)点P在线段AB上,点P的横坐标为m,
∴AP=m,
∵CQ=l,
∴BQ=3-l,
∵∠OAP=∠B=∠OPQ=90°,
∴∠APO+∠BPQ=∠APO+∠AOP=90°,
∴∠APO=∠BPQ,
∴△APO∽△BPQ,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
(3)存在,
如图,过点D作DE⊥OC于E,
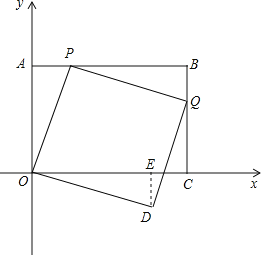
∵四边形ODQP是正方形,
∴OP=PQ=OD,
在△AOP与△BPQ中,
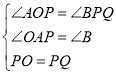 ,
,
∴△AOP≌△BPQ(AAS),
∴PB=OA=3,
∴AP=BP=1,
在△AOP与△OED中,
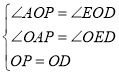 ,
,
∴△AOP≌△OEP(AAS),
∴OE=AO=3,DE=AP=1,
∴D(3,-1).
若点P在点B的右边,同理可得D(-3,7)
综上所述D(3,-1)或(-3,7)