题目内容
已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.
(1)如图①,当PA的长度等于 时,∠PAB=60°;当PA的长度等于 时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.坐标为(a,b),试求2 S1 S3-S22的最大值,并求出此时a,b的值.

(1)2, 或
或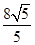 ;(2)当a=2时,b=2,2S1S3-S22有最大值是16.
;(2)当a=2时,b=2,2S1S3-S22有最大值是16.
【解析】
试题分析:(1)因为由是直径,可得∠APB=90°,要使∠PAB=60,即要∠PBA=30 ,即PA= PB=2,当PA=PD、PD=DA时,△PAD是等腰三角形,作辅助线DO
PB=2,当PA=PD、PD=DA时,△PAD是等腰三角形,作辅助线DO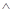 AP交PA于G,然后由正方形的性质、勾股定理易知△PAD△DGA,从而用对应边的相似比可得.
AP交PA于G,然后由正方形的性质、勾股定理易知△PAD△DGA,从而用对应边的相似比可得.
(2)要求2S1 S3-S22的最大值,只要先把S1、S2、S3用a,b表示,再根据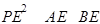 得到关系式,从而利用二次函数最大值概念求得.
得到关系式,从而利用二次函数最大值概念求得.
试题解析:(1)若∠PAB=60°,需∠PBA=30°,
∵AB是直径,
∴∠APB=90°,
则在Rt△PAB中,PA= AB=2,
AB=2,
∴当PA的长度等于2时,∠PAB=60°;
①若△PAD是等腰三角形,当PA=PD时,如图1,
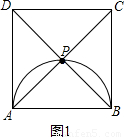
此时P位于正方形ABCD的中心O.
则PD⊥PA,PD=PA,
∴AD2=PD2+PA2=2PA2=16,
∴PA=2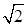
②当PD=DA时,以点D为圆心,DA为半径作圆与弧AB的交点为点P.如图2
连PD,令AB中点为O,再连DO,PO,DO交AP于点G,则△ADO≌△PDO,

∴DO⊥AP,AG=PG,
∴AP=2AG,
又∵DA=2AO,
∴AG=2OG,
设AG为2x,OG为x,
∴(2x)2+x2=4,
∴x=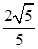
∴AG=2x=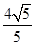 ,AP=
,AP=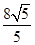
∴当PA的长度等于2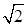 或
或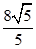 时,△PAD是等腰三角形.
时,△PAD是等腰三角形.
(2)如图,过点P分别作PE⊥AB,PF⊥AD,垂足分别为E、F,延长EP交BC于点G,则PG⊥BC.

∵P点坐标为(a,b),
∴PE=b,PF=a,PG=4-a
在△PAD、△PAB和△PBC中,

∵AB为直径
∴∠APB=90°
∴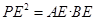 ,即
,即
∴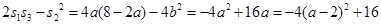
∴当a=2时,b=2,2S1S3-S22有最大值是16.
考点: 圆的综合题.



