题目内容
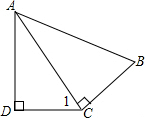如图，∠ADC=∠ACB=90°，∠1=∠B，AC=5，AB=6，则AD等于（ ）分析：根据条件可以直接证明△ADC∽△ACB，再根据相似三角形的性质就可以求出结论．
解答：解：∵∠ADC=∠ACB=90°，∠1=∠B，
∴△ADC∽△ACB，
∴
=
．
∵AC=5，AB=6，
∴
=
，
∴AD=
．
故选B．
∴△ADC∽△ACB，
∴
| AD |
| AC |
| AC |
| AB |
∵AC=5，AB=6，
∴
| AD |
| 5 |
| 5 |
| 6 |
∴AD=
| 25 |
| 6 |
故选B．
点评：本题考查了相似三角形的判定与相似三角形的性质的运用，在解答时证明三角形相似是关键．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
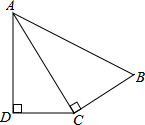如图，∠ADC=∠ACB=90°，∠ACD=∠B，AC=5，AB=6，则AD=
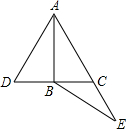如图，△ADC是等边三角形，B是DC边中点，E在AC延长线上，且CE=BC，请判断△ABE的形状并证明你的结论．
如图，△ADC是等边三角形，以点A为中心，把△ABD顺时针旋转60°得到△ACE．连接BE，则△ABE是什么特殊三角形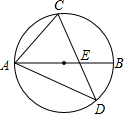
如图，△ADC的外接圆直径AB交CD于点E，已知∠C=65°，∠DEB=60°，求∠D的度数．