题目内容
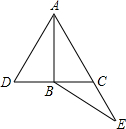如图，△ADC是等边三角形，B是DC边中点，E在AC延长线上，且CE=BC，请判断△ABE的形状并证明你的结论．分析：根据等边三角形的每个内角为60°及三线合一求出∠BAC的度数，再根据三角形的内角与外角的关系求出∠E=30°，从而得出△ABE是等腰三角形．
解答：解：∵B是DC边中点，
∴AB是等边三角形ADC的顶角平分线，
∴∠BAC=30°．
∵CB=CE，
∴∠CBE=∠CEB，
∵∠ACD=60°，
∴∠E=30°，
∴∠E=∠BAE，
∴△ABE为等腰三角形．
∴AB是等边三角形ADC的顶角平分线，
∴∠BAC=30°．
∵CB=CE，
∴∠CBE=∠CEB，
∵∠ACD=60°，
∴∠E=30°，
∴∠E=∠BAE，
∴△ABE为等腰三角形．
点评：本题考查了等边三角形的性质和等腰三角形的判定，利用等边三角形的每个内角是60°及三角形内角和外角的关系是解题的关键．
练习册系列答案
优生乐园系列答案
相关题目
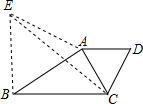
如图，△ADC是等边三角形，以点A为中心，把△ABD顺时针旋转60°得到△ACE．连接BE，则△ABE是什么特殊三角形
如图，△ADC是等边三角形，B是DC边中点，E在AC延长线上，且CE=BC，请判断△ABE的形状并证明你的结论．
