题目内容
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
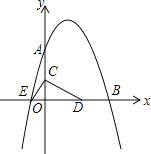
(1)求该抛物线的解析式及点E的坐标;
(2)若D点运动的时间为t,△CED的面积为S,求S关于t的函数关系式,并求出△CED的面积的最大值.
【答案】(1)y=﹣![]() x2+3x+8,E(﹣2,0);(2)当t=5时,S最大=
x2+3x+8,E(﹣2,0);(2)当t=5时,S最大=![]() .
.
【解析】
试题分析:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣![]() x2+bx+c即可求出抛物线的解析式为:y=﹣
x2+bx+c即可求出抛物线的解析式为:y=﹣![]() x2+3x+8;再令y=0,得:﹣
x2+3x+8;再令y=0,得:﹣![]() x2+3x+8=0,解方程可得点E的坐标;
x2+3x+8=0,解方程可得点E的坐标;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,然后由点A(0,8)、B(8,0),可得OA=8,OB=8,从而可得OD=8﹣t,然后令y=0,点E的坐标为(﹣2,0),进而可得OE=2,DE=2+8﹣t=10﹣t,然后利用三角形的面积公式即可求△CED的面积S与D点运动时间t的函数解析式为:S=﹣![]() t2+5t,然后转化为顶点式即可求出最值为:S最大=
t2+5t,然后转化为顶点式即可求出最值为:S最大=![]() .
.
解:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣![]() x2+bx+c得:
x2+bx+c得: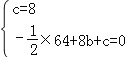 ,
,
解得:b=3,c=8,
故抛物线的解析式为:y=﹣![]() x2+3x+8,
x2+3x+8,
∵点A(0,8)、B(8,0),
∴OA=8,OB=8,
令y=0,得:﹣![]() x2+3x+8=0,
x2+3x+8=0,
解得:x1=8,x2=﹣2,
∵点E在x轴的负半轴上,
∴点E(﹣2,0),
∴OE=2;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,
∴OD=8﹣t,
∴DE=OE+OD=10﹣t,
∴S=![]() DEOC=
DEOC=![]() (10﹣t)t=﹣
(10﹣t)t=﹣![]() t2+5t,
t2+5t,
即S=﹣![]() t2+5t=﹣
t2+5t=﹣![]() (t﹣5)2+
(t﹣5)2+![]() ,
,
∴当t=5时,S最大=![]() .
.