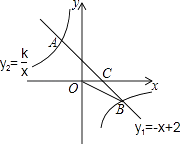题目内容
【题目】如图,直线m与直线n相交于点O,A、B两点同时从点O出发,点A以每秒x个单位长度沿直线n向左运动,点B以每秒y个单位长度沿直线m向上运动。
(1)若运动1s时,点B比点A多运动1个单位;运动2s时,点B与点A运动的路程和为6个单位,则x=_________,y=___________.
(2)如图,当直线m与直线n垂直时,设∠BAO和∠ABO的角平分线相交于点P.在点A、B在运动的过程中,∠APB的大小是否会发生变化?若不发生变化,请求出其值(写出主要过程);若发生变化,请说明理由.
(3)如图,将(2)中的直线n不动,直线m绕点O按顺时针方向旋转α(0<ɑ<90),其他条件不变.ⅰ)用含有α的式子表示∠APB的度数____________.
ⅱ)如果再分别作△ABO的两个外角∠BAC,∠ABD的角平分线相交于点Q,并延长BP、QA交于点M.则下列结论正确的是___________(填序号) .
①APB与∠Q互补;②∠Q与∠M互余;③∠APB-∠M为定值;④∠M-∠Q为定值.

【答案】(1) 1,2.(2) ∠APB的大小不会发生变化,![]() (3)ⅰ)
(3)ⅰ) ![]() ⅱ)①②③.
ⅱ)①②③.
【解析】
(1)根据题意列出方程组,解方程即可.
(2)∠APB的大小不会发生变化,![]() 根据三角形的内角和定理得到
根据三角形的内角和定理得到![]() 根据角平分线的性质可得
根据角平分线的性质可得![]() 根据三角形的内角和定理即可求出∠APB的度数.
根据三角形的内角和定理即可求出∠APB的度数.
(3)ⅰ)参照(2)中的步骤进行求解即可.
ⅱ)分别求出∠APB,∠Q,∠M的度数,进行判断即可.
(1)根据题意可得:
![]()
解得:![]()
故答案为:1,2.
(2) ∠APB的大小不会发生变化,![]()
![]() 直线m与直线n垂直,
直线m与直线n垂直,
![]()
![]()
![]() PA,PB分别是∠BAO和∠ABO的角平分线,
PA,PB分别是∠BAO和∠ABO的角平分线,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)ⅰ)根据题意可得![]()
![]()
![]() PA,PB分别是∠BAO和∠ABO的角平分线,
PA,PB分别是∠BAO和∠ABO的角平分线,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
故答案为:![]()
ⅱ) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 故①∠APB与∠Q互补正确.
故①∠APB与∠Q互补正确.
![]()
![]()
![]()
![]() 故②∠Q与∠M互余正确.
故②∠Q与∠M互余正确.
![]() 是定值,故③∠APB-∠M为定值正确.
是定值,故③∠APB-∠M为定值正确.
![]() 不是定值,故④∠M-∠Q为定值错误.
不是定值,故④∠M-∠Q为定值错误.
故答案为:①②③.

【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度.
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高73.5cm的课桌,它们是否配套?为什么?