题目内容
【题目】已知△ABC在平面直角坐标系中的位置如图所示，直线l过点M（3，0）且平行于y轴．
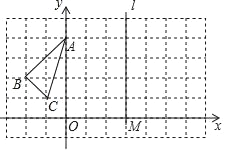
（1）作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标．
（2）如果点P的坐标是（﹣a，0），其中a＞0，点P关于y轴的对称点是P1，点P1关于直线l的对称点是P2，求P1P2的长．（用含a的代数式表示）
（3）通过计算加以判断，PP2的长会不会随点P位置的变化而变化．
【答案】（1）详见解析，A1（0，4）、B1（2，2）C1（1，1）；（2）当0＜a≤3时，P1P2=6﹣2a；当a＞3时，P1P2=2a﹣6；（3）PP2的长不会随点P位置的变化而变化．
【解析】
（1）如图1，分别作出点B、C关于y轴的对称点，再顺次连接可得；（2）P与P1关于y轴对称，利用关于y轴对称点的特点：纵坐标不变，横坐标变为相反数，求出P1的坐标，再由直线l的方程为直线x=3，利用对称的性质求出P2的坐标，即可PP2的长（本题分0＜a≤3和a＞3两种情况求解）；（3）根据以上两种情况，分别利用PP2=PP1+P1P2、PP2=PP1﹣P1P2计算可得结论．
（1）如图，△A1B1C1即为所求，
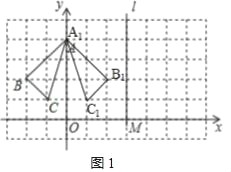
A1（0，4）、B1（2，2）C1（1，1）；
（2）①如图2，当0＜a≤3时，
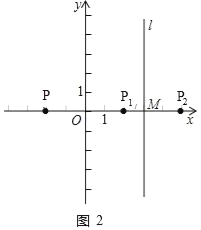
∵P与P1关于y轴对称，P（﹣a，0），
∴P1（a，0），
又∵P1与P2关于l：直线x=3对称，
设P2（x，0），可得：
=3，即x=6﹣a，
∴P2（6﹣a，0），
则PP2=6﹣a+a=6．
∴P1P2=6﹣2a；
②如图3，当a＞3时，
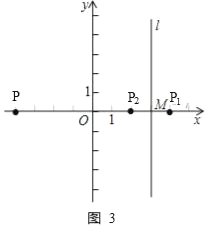
∵P与P1关于y轴对称，P（﹣a，0），
∴P1（a，0），
又∵P1与P2关于l：直线x=3对称，
设P2（x，0），可得：
=3，即x=6+a，
∴P2（6+a，0），
则PP2=6+a﹣a=6．
∴P1P2=2a﹣6.
综上所述，当0＜a≤3时，P1P2=6﹣2a；当a＞3时，P1P2=2a﹣6；
（3）当0＜a≤3时，PP2=PP1+P1P2=2a+6﹣2a=6；
当a＞3时，PP2=PP1﹣P1P2=2a﹣（2a﹣6）=6；
∴PP2的长不会随点P位置的变化而变化．
