Question

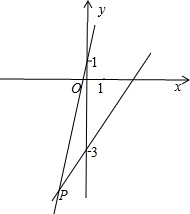
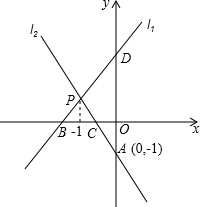
如图，直线l₁与l₂相交于点P，l₁的函数表达式y=2x+3，点P的横坐标为-1，且l₂交y轴于点A（0，-1）．
（1）求出点P的坐标；
（2）求出直线l₂的函数关系式；
（3）求l₁、l₂与x轴所围成的△PBC的面积．

Answer 1

（1）∵把x=-1，代入y=2x+3，得y=1，
∴点P（-1，1）

（2）设直线l₂的函数表达式为y=kx+b，把P（-1，1）、A（0，-1）分别代入y=kx+b，
得

1=-k+b b=-1

，
∴k=-2，b=-1．
∴直线l₂的函数表达式为y=-2x-1．

（3）把y=0代入y=2x+3，得x=-

3

2

，
∴B(-

3

2

，0)；
同理，把y=0代入y=-2x-1中，得x=-

1

2

，
∴C(-

1

2

，0)
∴BC=(-

1

2

)-(-

3

2

)=1，
又∵P（-1，1）
∴S_△PBC=

1

2

×1×1=

1

2