题目内容
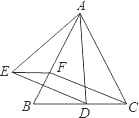
【题目】已知,四边形ABCD是正方形,∠MAN=90°,将∠MAN绕顶点A旋转,旋转角为∠DAM(0°<∠DAM<45°),AM交CD于点E,∠MAN的平分线与CB交于点G
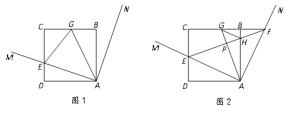
(1)证明:如图1,连接GE.求证:GE=DE+BG;
(2)探究:如图2,设AN交CB的延长线于点F,直线EF分别交AG,AB于点P,H.探究GH与AE的位置关系,并证明你的结论;
(3)应用:在图2中,若正方形的边长为6,BG=2,求GH的长.
【答案】(1)见解析;(2)GH∥AE,证明见解析;(3)![]()
【解析】
(1)延长CB交AN于点F,通过证△DAE≌△BAF和△EAG≌△FAG从而证得结论;(2)首先证明△PAH≌△PFG .则PH=PG ,从而∠PGH=45°. 又因为AP=EP,∠APE=90°. 所以∠PAE=45°.证得∠PGH=∠PAE,再根据平行线的判定得到GH∥AE;(3)设DE=![]() ,则CG=4,CE=6-
,则CG=4,CE=6-![]() ,GE=GF=2+
,GE=GF=2+![]() .在Rt△CEG中通过勾股定理求出x的值.再证△FBH∽△FCE,根据相似的性质即可求出BH的长,再在Rt△GBH中通过勾股定理求出GH的长.
.在Rt△CEG中通过勾股定理求出x的值.再证△FBH∽△FCE,根据相似的性质即可求出BH的长,再在Rt△GBH中通过勾股定理求出GH的长.
(1)证明:延长CB交AN于点F,
∵ABCD是正方形,∴AD=AB,∠DAB=∠D=∠ABF=90°.
∵∠MAN=90°,∴∠DAB=∠MAN.
∴∠DAB-∠EAB=∠MAN-∠EAB即:∠DAE=∠BAF.

∴△DAE≌△BAF.∴AE=AF.
又AG=AG,∠EAG=∠FAG.
∴△EAG≌△FAG .∴GE=GF.
而GF=BG+BF=BG+DE
∴GE=BG+DE.
(2)解: GH∥AE,证明如下:
∵AE=AF,AG平分∠EAF∴AG⊥EF,EP=FP.
∴∠APH=∠FPG=∠APE=90°,AP=![]() EF=EP=FP
EF=EP=FP
∴∠PFG+∠PGF=90又∵∠ABG=90°,∴∠PAH+∠PGF=90°.∴∠PAH=∠PFG.
∴△PAH≌△PFG .∴PH=PG .∴∠PGH=45°.
∵AP=EP,∠APE=90°. ∴∠PAE=45°.
∴∠PGH=∠PAE.∴GH∥AE.
(3)连接GE,由(1)知GE=GF,DE=BF.
设DE=![]() ,因为正方形边长为6,BG=2,
,因为正方形边长为6,BG=2,

∴CG=4,CE=6-![]() ,GE=GF=2+
,GE=GF=2+![]() .
.
在Rt△CEG中,CE2+CG2=GE2,
∴![]()
解得![]() ,即:DE=BF=3 .
,即:DE=BF=3 .
∴CE=6-3=3,CF=6+3=9 .
∵BH∥CE ∴△FBH∽△FCE ∴![]() .
.
∴BH=1
∵∠GBH=90° ∴GH=![]() .
.

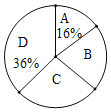
【题目】2020年4月是我国第32个爱国卫生月.某校九年级通过网课举行了主题为“防疫有我,爱卫同行”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
(1)本次调查一共随机抽取了____个参赛学生的成绩;
(2)表1中a=__;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是__;
(4)统计图中B组所占的百分比是_______;
(5)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生人数.
表1 知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A | 60≤x<70 | a |
B | 70≤x<80 | 10 |
C | 80≤x<90 | 14 |
D | 90≤x<100 | 18 |
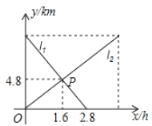
【题目】经销商购进某种商品,当购进量在20千克~50千克之间(含20千克和50千克)时,每千克进价是5元;当购进量超过50千克时,每千克进价是4元.此种商品的日销售量y(千克)受销售价x(元/千克)的影响较大,该经销商试销一周后获得如下数据:
x(元/千克) | 5 | 5.5 | 6 | 6.5 | 7 |
y(千克) | 90 | 75 | 60 | 45 | 30 |
解答下列问题:
(1)求出y关于x的一次函数表达式:
(2)若每天购进的商品能够全部销售完,且当日销售价不变,日销售利润为w元,那么销售价定为多少时,该经销商销售此种商品的当日利润最大?最大利润为多少元?此时购进量应为多少千克?(注:当日利润=(销售价-进货价)×日销售量).