题目内容
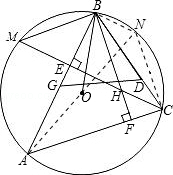
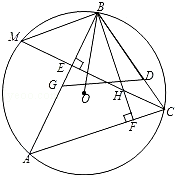
【题目】如图，O是△ABC的外接圆的圆心，∠ABC=60°，BF，CE分别是AC，AB边上的高且交于点H，CE交⊙O于M，D，G分别在边BC，AB上，且BD=BH，BG=BO，下列结论：①∠ABO=∠HBC；②ABBC=2BFBH；③BM=BD；④△GBD为等边三角形，其中正确结论的序号是（ ）
A.①② B.①③④ C.①②④ D.①②③④
【答案】D
【解析】
试题分析：①，延长AO交圆于点N，连接BN，可证明∠ABO=∠HBC．因此①正确；
②原式可写成
=
，无法直接用相似来求出，那么可通过相等的比例关系式来进行转换，不难发现三角形BEC中，∠ABC=60°，那么BC和BE存在倍数关系，即BC=2BE，因此如果证得
=，可发现这个比例关系式正好是相似三角形BEH和BAF的两组对应线段，因此本题的结论也是正确的．
③要证MB=BD，先看与BD相等的线段有哪些，不难通过相似三角形ABN和BFC（一组直角，∠OBA=∠OAB=∠FBC）得出
，将这个结论和②的结论进行置换即可得出：BD=BO=BH=BG，因此可证MB和圆的半径相等即可得出BM=BD的结论．如果连接NC，在三角形ANC中∠ANC=∠ABC=60°，因此AN=2NC，NC就是半径的长．通过相似三角形BME和CAE可得出
，而在直角三角形BEC中，BE：EC=tan30°，而在直角三角形ANC中，NC：AC=tan30°，因此
，即可得出BM=NC=BO=BD．因此该结论也成立．
④在③中已经得出了BD=BG=BO=BH，而∠ABC=60°，因此三角形BGD是等边三角形．本结论也成立．
因此四个结论都成立，
解：①延长AO交圆于点N，连接BN，则∠ABN=90°，又∠ACB=∠BNA，∠ABO=∠BAO，所以∠ABO=∠HBC．因此①正确；
②原式可写成
=
，∠ABC=60°，那么BC=2BE，因此
=，所以本题的结论也是正确的．
③∵△ABN∽△BFC（一组直角，∠OBA=∠OAB=∠FBC）∴，BD=BO=BH=BG，BM=BD．
连接NC，在三角形ANC中∠ANC=∠ABC=60°，∴AN=2NC，BE：EC=tan30°，
在直角三角形ANC中，NC：AC=tan30°，，∴BM=NC=BO=BD．
因此该结论也成立．
④在③中已经得出了BD=BG=BO=BH，而∠ABC=60°，因此三角形BGD是等边三角形．本结论也成立．
因此四个结论都成立，
故选D．
