题目内容
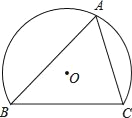
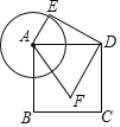
【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,
(1)当∠EAD=90°时,AF=________________.
(2)在E的整个运动过程中,AF的最大值是________________.
【答案】![]() 或5 ;
或5 ; ![]()
【解析】
(1)当∠EAD=90°时,分两种情况:①如图:当点E在BA的延长线上和当点E在点A下方,即![]() A于AB的交点就是点E时.根据旋转后大小不变和正方形边长相等,可以证明三角形全等,进而得出对应边相等,再根据勾股定理可得斜边AF的长;
A于AB的交点就是点E时.根据旋转后大小不变和正方形边长相等,可以证明三角形全等,进而得出对应边相等,再根据勾股定理可得斜边AF的长;
(2)先构造出全等三角形,判断出点F在AC的延长线上时,AF最大值,进而确定出点E的位置,再判断出AF最大时,点C在AF上,根据正方形的性质求出AC,从而得出AF的最大值.
解:(1)∠EAD=90°时,
①如图:当点E在BA的延长线上时,
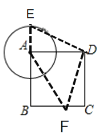
∵DE=DF DA=DC,
∴Rt△ADE≌Rt△CDF
∴AE=CF=1 BF=BC-CF=2
∴在Rt△ABF中,AF=![]() =
=![]() =
=![]() ;
;
②如图:当点E在点A下方,即![]() A于AB的交点就是点E时:
A于AB的交点就是点E时:

方法同①可得Rt△ADE≌Rt△CDF,AE=CF=1
∴BF=BC+CF=4
∴在Rt△ABF中,AF=![]() =
=![]() =5.
=5.
故答案为:![]() 或5 ;
或5 ;
(2)解:如图1,
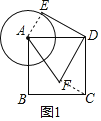
连接AE,CF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
由旋转知,DE=DF,∠EDF=90°,
∴∠ADE=∠CDF,
∴△ADE≌△CDF(SAS),
∴CF=AE=1,
∴点F的轨迹是以点C为圆心,半径为1圆,
∴点F在AC的延长线上时,AF最大;
如图,过点A作∠EAB=45°交⊙A于点E,此时旋转后AF最大,过点E作EG⊥AD交DA延长线于G,

在Rt△AEG中,AE=1,∠GAE=∠EAB=45°,
∴EG=AG=![]() ,
,
∵∠ADC=∠EDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
∴△ADE≌△CDF,
∴CF=AE=1,∠DCF=∠DAE=∠BAD+∠EAB=90°+45°=135°,
∴点C在线段AF上,
∴AF=AC+CF,
∵AC是边长为3的正方形的对角线,
∴AC=3![]() ,
,
∴AF=3![]() +1,
+1,
即:AF的最大值是3![]() +1,
+1,
故答案为:3![]() +1.
+1.

【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
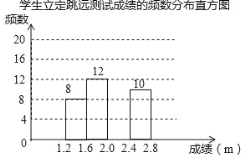
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有850名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?