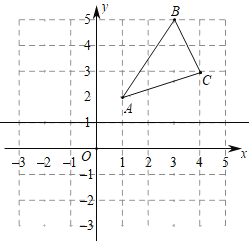��Ŀ����
����Ŀ��������ģ�ͣ�
��֪����ֱ�ǡ�ABC����ACB��90�㣬AC��CB������C����һ��ֱ��l������CA��CB�غϣ�������A��AD��l��D������B��BE��l�� E��
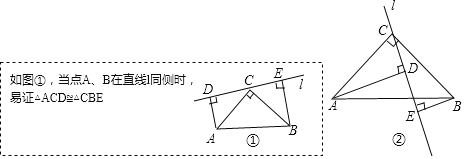
��1����ͼ��������A��B��ֱ��l���ʱ����֤����ACD�ա�CBE
��ģ��Ӧ�ã�
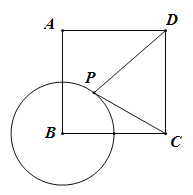
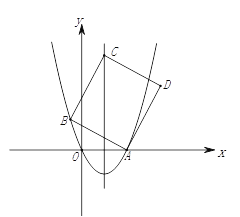
��ƽ��ֱ��������xOy�У���ֱ֪��l��y��kx��4k��kΪ������k��0����x�ύ�ڵ�A����y��ĸ����ύ�ڵ� B����ABΪ�ߡ�BΪֱ�Ƕ���������ֱ�ǡ�ABC��
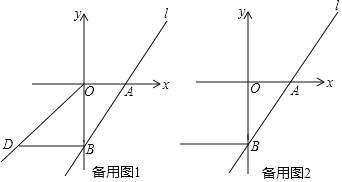
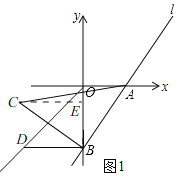
��2����ֱ��l�����㣨2����3��������C�ڵ�������ʱ����C������Ϊ�� ����
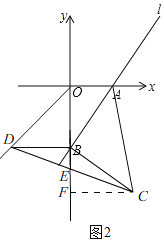
��3����D�Ǻ���y��x��x��0��ͼ���ϵĵ㣬��BD��x�ᣬ����C�ڵ�������ʱ������CD��y���ڵ�E����EB�ij���Ϊ�� ����
��4�����C������Ϊ��a��b����̽��a��b֮������ĵ�����ϵ��ֱ��д�����ۣ���������ĸk��
���𰸡���1�������������2��(��6����2)����3��2����4��a+ b=-4��b��a��4��
��������
��1������ͬ�ǵ��������жϳ���CAD����BCE����������AAS���ɵó����ۣ�
��2�������ֱ��l�Ľ���ʽ������ȷ������A��B���꣬���жϳ���ACD�ա�CBE�����ɵó����ۣ�
��3��ͬ��2���ķ����ɵá�OAB�ա�FBC���Ӷ���BF��OA��4����֤��BED�ա�FEC��AAS�������ɵõ��𰸣�
��4���ֵ�C�ڵڶ����ޣ��������͵������������������ȷ������A��B���꣬��ͬ��2����3���ķ���ȷ������C�����꣨��k��ʾ�������ɵó����ۣ�
��1���ߡ�ACB��90�㣬
���ACD+��ECB��90�㣬
��AD��l��BE��l��
���ADC����BEC��90�㣬
���ACD+��CAD����ACD+��BCE��90�㣬
���CAD����BCE��
��CA��CB��
���ACD�ա�CBE��AAS����
��2����ͼ1������C��CE��y���ڵ�E��
��ֱ��l��y��kx��4k������(2����3)��
��2k��4k����3��
��k��![]() ��
��
��ֱ��l�Ľ���ʽΪ��y��![]() x��6��
x��6��
��x��0����y����6��
��B(0����6)��
��OB��6��
��y��0����0��![]() x��6��
x��6��
��x��4��
��A(4��0)��
��OA��4��
ͬ��1���ķ����ã���OAB�ա�EBC��AAS����
��CE��OB��6��BE��OA��4��
��OE��OB��BE��6��4��2��
�ߵ�C�ڵ������ޣ�
��C(��6����2)��
�ʴ�Ϊ��(��6����2)��
��3����ͼ2��
����ֱ��l��y��kx��4k��
��x��0����y����4k��
��B(0����4k)��
��OB��4k��
��y��0����kx��4k��0��
��x��4��
��A(4��0)��
��OA��4��
����C��CF��y����F�����OAB�ա�FBC��AAS����
��BF��OA��4��CF��OB��4k��
��OF��OB+BF��4k+4��
�ߵ�C�ڵ������ޣ�
��C(4k��-4k-4)��
��B(0����4k)��
��BD��x�ᣬ��D��y��x�ϣ�
��D(��4k����4k)��
��BD��4k��CF��
��CF��y����F��
���CFE��90�㣬
��BD��x�ᣬ
���DBE��90�㣽��CFE��
�ߡ�BED����FEC��
���BED�ա�FEC��AAS����
��BE��EF��![]() BF��2��
BF��2��
�ʴ�Ϊ��2��
��4���ٵ���C�ڵ�������ʱ���ɣ�3��֪��C(4k��-4k-4)��
��C(a��b)��
��a��4k��b��-4k-4��
��a+ b=-4��
�ڵ���C�ڵ�������ʱ���ɣ�3��֪��B(0����4k)��A(4��0)��
��OB��4k��OA��4��
��ͼ1���ɣ�2��֪����OAB�ա�EBC��AAS����
��CE��OB��4k��BE��OA��4��
��OE��OB��BE��4k��4��
��C(��4k��-4k+4)��
��C(a��b)��
��a����4k��b��-4k+4��
��b��a��4��
�۵���C�ڵڶ�����ʱ����ͼ3���ɣ�3��֪��B(0����4k)��A(4��0)��
��OB��4k��OA��4��
�ߡ�OAB�ա�MBC��AAS����
��CM��OB��4k��BM��OA��4��
��OM��BM��BO��4��4k��
��C(��4k��4��4k)��
��C(a��b)��
��a����4k��b��4��4k��
��b��a��4��
�ܵ�C�������ڵ�һ���ޣ�
����������a+ b=-4��b��a��4��
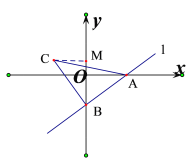
ͼ3

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�