Question

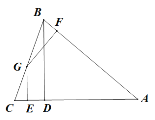
【题目】如图，在等腰△中，，，于点，点是底边上一点，过点向两腰作垂线段，垂足分别为、，若，，则的长度为（ ）.

A. B. C. D.

Answer 1

【答案】C

【解析】

过G作GP⊥BD于P，证明四边形PGED是矩形，得到证明

△BPG≌△GFB，得到根据锐角三角函数的定义即可求出的长度.

证明：过G作GP⊥BD于P，

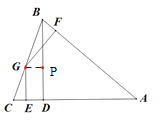
∵BD⊥AC，GF⊥AC，

∴PG∥DE,GE∥PD(垂直于同一条直线的两条直线互相平行)，

∴四边形PGED是平行四边形(两条对边互相平行的四边形是平行四边形)；

又∵

∴四边形PGED是矩形(有一个角是直角的平行四边形是矩形)，

∴ (矩形的对边相等)①

∵四边形PGED是矩形

∴PG∥DE,即PG∥AC，

∴∠BGP=∠C(两条直线平行,同位角相等)，

又∵AB=AC(已知)

∴∠ABC=∠C(等腰三角形的两底角相等)，

∴∠BGP =∠ABC(等量代换)

∵在△BPG与△GFB中，

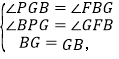
∴△BPG≌△GFB (AAS)

∴

解得：

故选：C.