题目内容
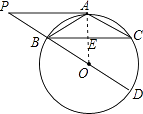
【题目】如图,⊙O中,点A为 ![]() 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P. 
(1)求证:PA是⊙O的切线;
(2)若 ![]() ,AB=6,求sin∠ABD的值.
,AB=6,求sin∠ABD的值.
【答案】
(1)证明:连结AO,交BC于点E.
∵点A是 ![]() 的中点
的中点
∴AO⊥BC,
又∵AP∥BC,
∴AP⊥AO,
∴AP是⊙O的切线
(2)解:∵AO⊥BC, ![]() ,
,
∴ ![]() ,
,
又∵AB=6
∴ ![]() ,
,
∵OA=OB
∴∠ABD=∠BAO,
∴ ![]() .
.
【解析】(1)根据垂径定理得出AO⊥BC,进而根据平行线的性质得出AP⊥AO,即可证得结论;(2)根据垂径定理得出BE=2 ![]() ,在RT△ABE中,利用锐角三角函数关系得出sin∠BAO=
,在RT△ABE中,利用锐角三角函数关系得出sin∠BAO= ![]() ,再根据等腰三角形的性质得出∠ABD=∠BAO,即可求得求sin∠ABD=sin∠BAO=
,再根据等腰三角形的性质得出∠ABD=∠BAO,即可求得求sin∠ABD=sin∠BAO= ![]() .
.
【考点精析】掌握切线的判定定理是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目