��Ŀ����
����Ŀ��������֤���� ��ͼ���ڷž���ֽƬABCD�����ֽƬECGF��ʹB��C��G������һ��ֱ���ϣ�CE�ڱ�CD�ϣ�����AF����MΪAF���е㣬����DM��EM��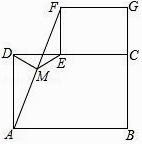
��1���Բ���д��DM��EM��������ϵ����֤����Ľ��ۣ� ��չ�����죺
��2��������������֤�����е�ֽƬ����������ֽƬABCD��������ֽƬECGF�������������䣬��1���еĽ����Ƿ���Ȼ��������ֱ��д������жϣ�
���𰸡�
��1���⣺���ۣ�DM=EM��
���ɣ���ͼ1���ӳ�EM��AD�ڵ�H��
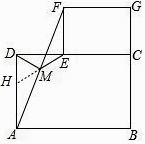
���ı���ABCD��ECGF�Ǿ��Σ�
��AD//EF��
���EFM=��HAM��
�֡ߡ�FME=��AMH��FM=AM��
�ڡ�FME�͡�AMH�У�
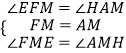 ��
��
���FME�ա�AMH��
��HM=EM��
��ֱ�ǡ�HDE�У�HM=EM��
��DM=HM=EM��
��DM=EM��
��2���⣺��������֤���������ƣ�
����������1�����ۣ�DM=EM��ֻҪ֤����FME�ա�AMH���Ƴ�HM=EM����ֱ�ǡ�HDE������б�����ߵ����ʼ���֤������2�����۲��䣮֤���������ƣ�
�����㾫�������þ��ε����ʺ������ε��ж���������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����ȣ����ж�һ���ı����Ǿ��Σ����ж�����һ���ڱ���ȣ����ж�һ���ı��������Σ����ж�����һ������ֱ�ǣ�