题目内容
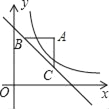
【题目】如图,已知直线![]() :
:![]() 与x轴交于点B,直线
与x轴交于点B,直线![]()
![]() 与y轴交于点C,且它们都经过点D(1,
与y轴交于点C,且它们都经过点D(1,![]() )
)
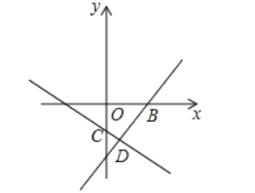

(1)求C、B两点的坐标;
(2)设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值;
(3)在(2)的条件下,在第四象限内,以CP为腰作等腰直角三角形△CPQ,请直接写出点Q的坐标.
【答案】(1)B (3,0),C (0,2);(2)t=5;(3)Q(7,5).
【解析】
(1)根据待定系数法,可得函数解析式,根据自变量与函数值的对应关系,可得B、C点坐标;
(2)根据面积的和差,可得关于t的方程,根据解方程,可得答案;
(3)根据全等三角形的判定与性质,可得PF,PQ的长,根据点的坐标的意义,可得Q点的坐标.
(1)将(1, ![]() )代入
)代入![]() ,解得n=4,
,解得n=4,
即![]() ,当y=0时,
,当y=0时, ![]() .
.
解得x=3,
即B点坐标为(3,0);
将(1, ![]() )代入
)代入![]() ,解得m=2,
,解得m=2,
即![]() ,当x=0时,
,当x=0时, ![]() .
.
即C点坐标为(0,2);
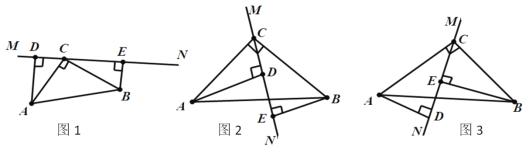
(2)连接PC,PD,如图1,

S![]() =
=![]() (t3)×|
(t3)×|![]() |=
|=![]() (t3);
(t3);
当y=0时, ![]() ,解得x=3,即E点坐标为(3,0).
,解得x=3,即E点坐标为(3,0).
S![]() =S
=S![]() S
S![]() =
=![]() (t+3)×
(t+3)×![]()
![]() ×(t+3)×|2|=
×(t+3)×|2|=![]() (t+3)
(t+3)
由△BDP和△CDP的面积相等,得
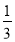 (t+3)=
(t+3)=![]() (t3).
(t3).
解得t=5.
(3)如图2,
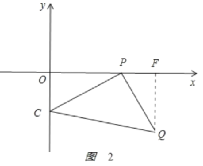
作QF⊥x轴于F点.
由△CPQ是等腰直角三角形,得
CP=PQ,∠CPQ=90°.
∠OPC+∠PCO=90°,∠OPC+∠QPF=90°,
∴∠PCO=∠QPF.
在△CPO和△PQF中,
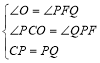 ,
,
∴△CPO≌△PQF(AAS),
∴PF=OC=2,FQ=OP=5,
Q点的横坐标为5+2=7,Q点的纵坐标为5,
即Q(7,5).

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目