题目内容
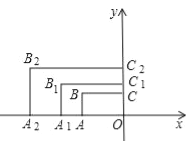
【题目】如图,将![]() 放在平面直角坐标系中,点
放在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() 动点
动点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以1个单位长度的速度运动,同一时间,动点
以1个单位长度的速度运动,同一时间,动点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以每秒2个单位长度的速度运动,当其中一点到达端点时,另一点也随之停止运动.过点
以每秒2个单位长度的速度运动,当其中一点到达端点时,另一点也随之停止运动.过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() 秒(t
秒(t![]() .
.

(Ⅰ)用含![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅱ)①是否存在![]() 的值,使四边形
的值,使四边形![]() 为平行四边形?若存在,求出
为平行四边形?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
②是否存在![]() 的值,使四边形
的值,使四边形![]() 为菱形?若存在,求出
为菱形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅲ)在整个运动过程中,求出线段![]() 的中点
的中点![]() 所经过的路径长.(直接写出结果即可).
所经过的路径长.(直接写出结果即可).
【答案】(Ⅰ)![]() ;(Ⅱ)①存在,
;(Ⅱ)①存在,![]() ;②不存在,四边形
;②不存在,四边形![]() 不能为菱形,见解析;(Ⅲ)线段
不能为菱形,见解析;(Ⅲ)线段![]() 中点
中点![]() 所经过的路径长为
所经过的路径长为![]() .
.
【解析】
(Ⅰ)根据题意得到OQ=2t,AP=t,求出BQ=8-2t,证明△ADP∽△ABO,根据相似三角形的性质求出PD;
(Ⅱ)①根据平行四边形的判定方法得出BQ=DP,列出关于t的方程,解方程即可;②先根据勾股定理得出AB的长,再根据平行线分线段成比例定理可得AD=![]() ,
,![]() ,根据①中
,根据①中![]() 是平行四边形时t的值求出PD和BD的值即可判定.
是平行四边形时t的值求出PD和BD的值即可判定.
(Ⅲ)根据点Q在BO上运动,点P在AO上运动,得出线段PQ的中点M的运动路径为一条线段,确定点Q分别与点O、点B重合时PQ的中点M的位置,再进一步求解可得.
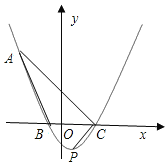
解:(I)∵点![]() ,点
,点![]() ,
,
∴![]() ,
, ![]() ,
,
且由题意,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]() .
.
(Ⅱ)①∵![]() ,若
,若![]() ,
,
∴则四边形![]() 是平行四边形,
是平行四边形,
即![]() ,解得:
,解得:![]() .
.
∴当![]() 时,∴四边形
时,∴四边形![]() 为平行四边形.
为平行四边形.
②不存在,理由如下:
∵![]() ,
,![]() ,
,
∴在![]() 中,
中, ![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,![]()
∴当![]() ,四边形
,四边形![]() 为平行四边形时,
为平行四边形时,
![]() ,
,![]()
∴![]() ,
,
∴四边形PDBC不能为菱形.
(Ⅲ))∵点Q在BO上运动,点P在AO上运动,
∴线段PQ的中点M的运动路径为一条线段,
∵当Q在点O时,点P在点A处,
∵点M为PQ的中点
∴OM=![]() PQ=
PQ=![]() ,
,
∵当Q在点B时,AP=4,则OP=2
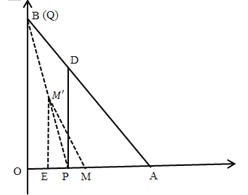
此时,连接PQ,取PQ的中点![]() ,过
,过![]() 作
作![]()
![]() OA于E,
OA于E,
∴OE=1,
∴EM=2,
∵AO⊥BO、![]() E⊥OA,
E⊥OA,
∴![]() E∥BO,
E∥BO,
∵![]() 为PQ的中点,
为PQ的中点,
∴![]() E为△BOP的中位线,
E为△BOP的中位线,
∴![]() E=
E=![]() BO=4,
BO=4,
点M的运动路径为M![]() =
=![]() =2
=2![]() .
.

【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.