Question

【题目】已知AB是⊙O的直径，弦CD⊥AB于点E．

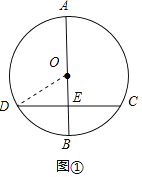
（1）如图①，若CD＝8，BE＝2，求⊙O的半径；

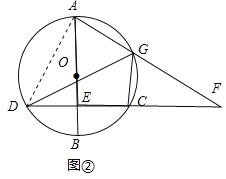
（2）如图②，点G是上一点，AG的延长线与DC的延长线交于点F，求证：∠AGD＝∠FGC．

Answer 1

【答案】（1）5 （2）见解析

【解析】

（1）连接OD，设⊙O的半径为r，根据垂径定理求出DE，根据勾股定理列式计算；

（2）连接AD，根据垂径定理得到 ，根据圆周角定理得到∠ADC＝∠AGD，根据圆内接四边形的性质得到∠ADC＝∠FGC，等量代换即可证明．

（1）解：如图①，连接OD，

设⊙O的半径为r，则OE＝r﹣2，

∵AB是⊙O的直径，弦CD⊥AB，

∴DE＝CD＝4，

在Rt△OED中，OD2＝OE2+DE2，即r2＝（r﹣2）2+42，

解得：r＝5，即⊙O的半径为5；

（2）证明：如图②，连接AD，

∵AB是⊙O的直径，弦CD⊥AB，

∴，

∴∠ADC＝∠AGD，

∵四边形ADCG是圆内接四边形，

∴∠ADC＝∠FGC，

∴∠FGC＝∠AGD．