题目内容
 在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动(点M可以与点A重合,点N可以与点C重合),求线段AT长度的最大值与最小值的和(计算结果不取近似值).
在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动(点M可以与点A重合,点N可以与点C重合),求线段AT长度的最大值与最小值的和(计算结果不取近似值).
解:当点M与点A重合时,AT取得最大值,
由轴对称可知,AT=AB=6;
当点N与点C重合时,AT取得最小值,
过点C作CD⊥l于点D,连结CT,则四边形ABCD为矩形,
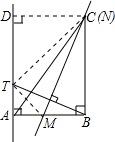
∴CD=AB=6,
由轴对称可知,CT=BC=8,
在Rt△CDT中,CD=6,CT=8,
则DT=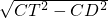 =
= ,
,
∴AT=AD-DT=8- ,
,
综上可得:线段AT长度的最大值与最小值的和为 .
.
分析:首先确定AT取得最大及最小时,点M、N的位置,然后分别求出每种情况下AT的值,继而可得线段AT长度的最大值与最小值的和.
点评:本题考查了翻折变换的知识,解答本题的关键是找到AT取得最大值、最小值的两个极值点,有一定难度,注意翻折前后对应边相等.
由轴对称可知,AT=AB=6;
当点N与点C重合时,AT取得最小值,
过点C作CD⊥l于点D,连结CT,则四边形ABCD为矩形,

∴CD=AB=6,
由轴对称可知,CT=BC=8,
在Rt△CDT中,CD=6,CT=8,
则DT=
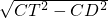 =
= ,
,∴AT=AD-DT=8-
 ,
,综上可得:线段AT长度的最大值与最小值的和为
 .
.分析:首先确定AT取得最大及最小时,点M、N的位置,然后分别求出每种情况下AT的值,继而可得线段AT长度的最大值与最小值的和.
点评:本题考查了翻折变换的知识,解答本题的关键是找到AT取得最大值、最小值的两个极值点,有一定难度,注意翻折前后对应边相等.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 如图,在三角形纸片ABC中,∠ACB=90°,BC=3,AB=6.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CE的长度为( )
如图,在三角形纸片ABC中,∠ACB=90°,BC=3,AB=6.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CE的长度为( ) (2012•惠山区一模)如图在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上移动,则线段AP长度的最大值与最小值的差为
(2012•惠山区一模)如图在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上移动,则线段AP长度的最大值与最小值的差为 如图,在三角形纸片ABC中,AB=6,BC=8,AC=4.沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
如图,在三角形纸片ABC中,AB=6,BC=8,AC=4.沿虚线剪下的涂色部分的三角形与△ABC相似的是( )



 (2013•大兴区二模)在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动(点M可以与点A重合,点N可以与点C重合),求线段AT长度的最大值与最小值的和(计算结果不取近似值).
(2013•大兴区二模)在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动(点M可以与点A重合,点N可以与点C重合),求线段AT长度的最大值与最小值的和(计算结果不取近似值). 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕翻折△ABC,使AB的一部分与BC重合,A与BC延长线上的点D重合,则线段AD的长度为( )
如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕翻折△ABC,使AB的一部分与BC重合,A与BC延长线上的点D重合,则线段AD的长度为( )