题目内容
 (2012•惠山区一模)如图在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上移动,则线段AP长度的最大值与最小值的差为
(2012•惠山区一模)如图在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上移动,则线段AP长度的最大值与最小值的差为| 7 |
| 7 |
分析:关键在于找到两个极端,即AP取最大或最小值时,点M或N的位置.经实验不难发现,分别求出点M与A重合时,AP取最大值3和当点N与C重合时,AP的最小值4-
所以可求线段AP长度的最大值与最小值之差.
| 7 |
解答: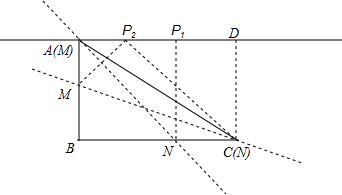 解:如图,过点C作CD⊥直线l交l于点D,
解:如图,过点C作CD⊥直线l交l于点D,
则四边形ABCD为矩形,通过操作知,当折叠过点A时,即点M与点A重合时,AP的值最大,
此时记为点P1,易证四边形ABNP1为正方形,
由于AC=5,BC=4,
故AB=
=
=3,
当折叠MN过点C时,AP的值最小,此时记为点P2,
由于P2C=BC=4,AB=CD=3,
故P2D=
=
,
故此时AP2=AD-P2D=4-
,
线段AP长度的最大值与最小值的差为:3-(4-
)=3-4+
=
-1.
故答案为:
-1.
 解:如图,过点C作CD⊥直线l交l于点D,
解:如图,过点C作CD⊥直线l交l于点D,则四边形ABCD为矩形,通过操作知,当折叠过点A时,即点M与点A重合时,AP的值最大,
此时记为点P1,易证四边形ABNP1为正方形,
由于AC=5,BC=4,
故AB=
| AC2-BC2 |
| 52-42 |
当折叠MN过点C时,AP的值最小,此时记为点P2,
由于P2C=BC=4,AB=CD=3,
故P2D=
| 42-32 |
| 7 |
故此时AP2=AD-P2D=4-
| 7 |
线段AP长度的最大值与最小值的差为:3-(4-
| 7 |
| 7 |
| 7 |
故答案为:
| 7 |
点评:本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识,难度稍大,学生主要缺乏动手操作习惯,单凭想象容易造成错误.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2012•惠山区一模)如图,已知AB∥CD,∠AEF=80°,则∠DCF为
(2012•惠山区一模)如图,已知AB∥CD,∠AEF=80°,则∠DCF为