题目内容
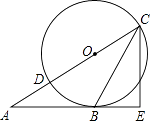
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.﹣4
B.4
C.﹣2
D.2
【答案】A
【解析】解:过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D. 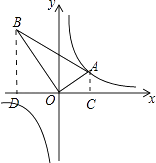
设点A的坐标是(m,n),则AC=n,OC=m,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠DBO+∠BOD=90°,
∴∠DBO=∠AOC,
∵∠BDO=∠ACO=90°,
∴△BDO∽△OCA,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵OB=2OA,
∴BD=2m,OD=2n,
因为点A在反比例函数y= ![]() 的图象上,则mn=1,
的图象上,则mn=1,
∵点B在反比例函数y= ![]() 的图象上,B点的坐标是(﹣2n,2m),
的图象上,B点的坐标是(﹣2n,2m),
∴k=﹣2n2m=﹣4mn=﹣4.
故选A.
要求函数的解析式只要求出B点的坐标就可以,过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.根据条件得到△ACO∽△ODB,得到: ![]() =
= ![]() =
= ![]() =2,然后用待定系数法即可.
=2,然后用待定系数法即可.

练习册系列答案
相关题目
【题目】国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
类别 | 彩电 | 冰箱 | 洗衣机 |
进价(元/台) | 2000 | 1600 | 1000 |
售价(元/台) | 2300 | 1800 | 1100 |
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?