题目内容
 如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.求证:△PCQ为等边三角形.
分析:由C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,利用SAS易证得△ACD≌△BCE,继而可证得△ACP≌△BCQ,则可得CP=CQ,又由∠BCD=60°,即可证得:△PCQ为等边三角形.
解答:证明:∵△ABC和△CDE是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
在△ACP和△BCq中,
,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,
∴△PCQ为等边三角形.
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
在△ACP和△BCq中,
|
∴△ACP≌△BCQ(ASA),
∴CP=CQ,
∴△PCQ为等边三角形.
点评:此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有
24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有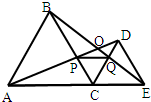 10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( ) 15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )
15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( ) 如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论:
如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论: