题目内容
【题目】已知:关于x的方程x2+2kx+k2﹣6=0
(1)证明:方程有两个不相等的实数根;
(2)如果方程有一个根为2,试求2k2+8k+2018的值.
【答案】(1)见解析;(2)2022.
【解析】
(1)计算判别式△=24,然后根据判别式的意义得到结论;
(2)把x=2代入方程得k2+4k=2,再把2k2+8k+2018变形为2(k2+4k)+2018,然后利用整体代入的方法计算.
(1)证明:△=(2k)2﹣4(k2﹣6)=24>0,
所以方程有两个不相等的实数根;
(2)把x=2代入方程得4+4k+k2﹣6=0,
所以k2+4k=2,
所以2k2+8k+2018=2(k2+4k)+2018=2×2+2018=2022.

练习册系列答案
相关题目
【题目】某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
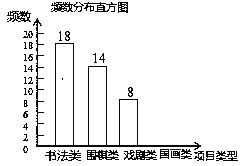
根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?