题目内容
在半径为l的⊙O中,弦AB,AC分别是
和
,则∠BAC的度数为( )
| 3 |
| 2 |
分析:由题意,半径为1,弦AB、AC分别是
、
,作OM⊥AB,ON⊥AC,根据垂径定理可求出AM与AN的长度,然后分别在直角三角形AOM与直角三角形AON中,利用余弦函数,可求出∠OAM=45°,∠OAN=30°,然后根据AC与AB的位置情况分两种,如图所示:故∠BAC的度数为45°+30°或45°-30°,问题可求.
| 2 |
| 3 |
解答:解:作OM⊥AB,ON⊥AC;由垂径定理,可得AM=
AB,AN=
AC,
∵弦AB、AC分别是
、
,
∴AM=
,AN=
;
∵半径为1,
∴OA=1;
∵
=
,
∴∠OAM=45°;
同理,∵
=
,
∴∠OAN=30°;
∴∠BAC=∠OAM+∠OAN或∠OAM-∠OAN
∴∠BAC=75°或15°.
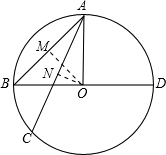
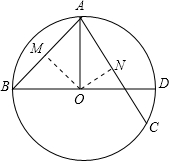
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
∵弦AB、AC分别是
| 3 |
| 2 |
∴AM=
| ||
| 2 |
| ||
| 2 |
∵半径为1,
∴OA=1;
∵
| AM |
| OA |
| ||
| 2 |
∴∠OAM=45°;
同理,∵
| AN |
| OA |
| ||
| 2 |
∴∠OAN=30°;
∴∠BAC=∠OAM+∠OAN或∠OAM-∠OAN
∴∠BAC=75°或15°.


故选D.
点评:此题主要考查了垂径定理、勾股定理以及三角形函数.本题综合性强,关键是画出图形,作好辅助线,利用垂径定理和直角三角形的特殊余弦值求得角的度数,注意要考虑到两种情况,不要漏解.

练习册系列答案
相关题目