题目内容
在半径为2的圆中，已知弦的长为2
，则这条弦与圆心的距离为
| 3 |
1
1
．分析：过O作OP⊥AB于P，连接OB，根据垂径定理求出BP，根据勾股定理求出OP即可．
解答：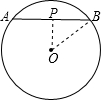
解：过O作OP⊥AB于P，连接OB，则OP的长度是弦AB与圆心的距离，
∵OP⊥AB，OP过O，
∴PB=
AB=
，
在Rt△OPB中，OB=2，PB=
，由勾股定理得：OP=
=1，
故答案为：1．
解：过O作OP⊥AB于P，连接OB，则OP的长度是弦AB与圆心的距离，∵OP⊥AB，OP过O，
∴PB=
| 1 |
| 2 |
| 3 |
在Rt△OPB中，OB=2，PB=
| 3 |
22-(
|
故答案为：1．
点评：本题考查了勾股定理，垂径定理的应用，主要考查学生运用定理进行计算和推理的能力．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
，则这条弦与圆心的距离为________．
，则弦AB的长为________．