题目内容
a、b是实数,如果已知
-
-3=0,且b4+b2-3=0,那么
的值是( )
| 4 |
| a4 |
| 2 |
| a2 |
| a4b4+4 |
| a4 |
| A、6 | B、7 | C、8 | D、9 |
分析:解法一:假设m=
,n=b2将
-
-3=0转化为一元二次方程m2-m-3=0,b4+b2-3=0转化为一元二次方程n2+n-3=0
利用公式法解这两个一元二次方程,得到m、n的值(不合题意,舍去).
将
转化为m2+n2,再进一步转化(m+n)2-2mn,用完全平方公式与平方差公式即可求解.
解法二:假设m=-
,n=b2,则根据已知与一元二次方程的根与系数的关系,那么m、n可以看作是方程x2+x-3=0的两个根
则m+n=-1,mn=-3
该式
可变换为m2+n2=(m+n)2-2mn,至此问题得以解决.
| 2 |
| a2 |
| 4 |
| a4 |
| 2 |
| a2 |
利用公式法解这两个一元二次方程,得到m、n的值(不合题意,舍去).
将
| a4b4+4 |
| a4 |
解法二:假设m=-
| 2 |
| a2 |
则m+n=-1,mn=-3
该式
| a4b4+4 |
| a4 |
解答:解:解法一:令m=
,n=b2
则
-
-3=0,转化为m2-m-3=0,b4+b2-3=0转化为n2+n-3=0,
解方程m2-m-3=0得m=
或m=
,
由于m=
>0,m=
,
同理解方程n2+n-3=0得n=
,n=
(不合题意,舍去),
所以m=
,n=
,
因而
=b4+
=m2+n2=(m+n)2-2mn=(
2-2×3=7;
故选B.
解法二:设m=-
,n=b2,则根据题意m、n可以看作是方程x2+x-3=0的两个根,
∴m+n=-1,mn=-3,
=(-
)2+(b2)2,
=m2+n2,
=(m+n)2-2mn,
=(-1)2-2×(-3),
=1+6,
=7.
故选B.
| 2 |
| a2 |
则
| 4 |
| a4 |
| 2 |
| a2 |
解方程m2-m-3=0得m=
1+
| ||
| 2 |
1-
| ||
| 2 |
由于m=
| 2 |
| a2 |
1+
| ||
| 2 |
同理解方程n2+n-3=0得n=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
所以m=
1+
| ||
| 2 |
-1+
| ||
| 2 |
因而
| a4b4+4 |
| a4 |
| 4 |
| a4 |
| 13) |
故选B.
解法二:设m=-
| 2 |
| a2 |
∴m+n=-1,mn=-3,
| a4b4+4 |
| a4 |
| 2 |
| a2 |
=m2+n2,
=(m+n)2-2mn,
=(-1)2-2×(-3),
=1+6,
=7.
故选B.
点评:这道题目确实很好,也很难,可谓是一道综合题,涉及到一元二次方程根与系数的关系求解、换元法、平方差公式、完全平方公式,即使做为大题出现也不为过.同学们一定要重视本题的解题思路.对于解法二具有一定层次的同学可以参考.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.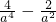 -3=0,且b4+b2-3=0,那么
-3=0,且b4+b2-3=0,那么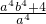 的值是
的值是