题目内容
(2012•苏州)如图,已知抛物线y=
x2-
(b+1)x+
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(1)点B的坐标为
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三 角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
| 1 |
| 4 |
| 1 |
| 4 |
| b |
| 4 |
(1)点B的坐标为
(b,0)
(b,0)
,点C的坐标为(0,
)
| b |
| 4 |
(0,
)
(用含b的代数式表示);| b |
| 4 |
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三
 角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.分析:(1)令y=0,即y=
x2-
(b+1)x+
=0,解关于x的一元二次方程即可求出A,B横坐标,令x=0,求出y的值即C的纵坐标;
(2)存在,先假设存在这样的点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形.设点P的坐标为(x,y),连接OP,过P作PD⊥x轴,PE⊥y轴,垂足分别为D、E,利用已知条件证明△PEC≌△PDB,进而求出x和y的值,从而求出P的坐标;
(3)存在,假设存在这样的点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似,有条件可知:要使△QOA与△QAB相似,只能∠QAO=∠BAQ=90°,即QA⊥x轴;要使△QOA与△OQC相似,只能∠QCO=90°或∠OQC=90°;再分别讨论求出满足题意Q的坐标即可.
| 1 |
| 4 |
| 1 |
| 4 |
| b |
| 4 |
(2)存在,先假设存在这样的点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形.设点P的坐标为(x,y),连接OP,过P作PD⊥x轴,PE⊥y轴,垂足分别为D、E,利用已知条件证明△PEC≌△PDB,进而求出x和y的值,从而求出P的坐标;
(3)存在,假设存在这样的点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似,有条件可知:要使△QOA与△QAB相似,只能∠QAO=∠BAQ=90°,即QA⊥x轴;要使△QOA与△OQC相似,只能∠QCO=90°或∠OQC=90°;再分别讨论求出满足题意Q的坐标即可.
解答:解:(1)令y=0,即y=
x2-
(b+1)x+
=0,
解得:x=1或b,
∵b是实数且b>2,点A位于点B的左侧,
∴点B的坐标为(b,0),
令x=0,
解得:y=
,
∴点C的坐标为(0,
),
故答案为:(b,0),(0,
);
(2)存在,
假设存在这样的点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形.
设点P的坐标为(x,y),连接OP.
则S四边形PCOB=S△PCO+S△POB=
•
•x+
•b•y=2b,
∴x+4y=16.
过P作PD⊥x轴,PE⊥y轴,垂足分别为D、E,
∴∠PEO=∠EOD=∠ODP=90°.
∴四边形PEOD是矩形.
∴∠EPD=90°.
∴∠EPC=∠DPB.
∴△PEC≌△PDB,∴PE=PD,即x=y.
由
解得
由△PEC≌△PDB得EC=DB,即
-
=b-
,
解得b=
>2符合题意.
∴P的坐标为(
,
);
(3)假设存在这样的点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似.
∵∠QAB=∠AOQ+∠AQO,
∴∠QAB>∠AOQ,∠QAB>∠AQO.
∴要使△QOA与△QAB相似,只能∠QAO=∠BAQ=90°,即QA⊥x轴.
∵b>2,
∴AB>OA,
∴∠Q0A>∠ABQ.
∴只能∠AOQ=∠AQB.此时∠OQB=90°,
由QA⊥x轴知QA∥y轴.
∴∠COQ=∠OQA.
∴要使△QOA与△OQC相似,只能∠QCO=90°或∠OQC=90°.
(I)当∠OCQ=90°时,△CQO≌△QOA.
∴AQ=CO=
.
由AQ2=OA•AB得:(
)2=b-1.
解得:b=8±4
.
∵b>2,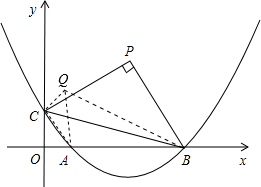
∴b=8+4
.
∴点Q的坐标是(1,2+
).
(II)当∠OQC=90°时,△OCQ∽△QOA,
∴
=
,即OQ2=OC•AQ.
又OQ2=OA•OB,
∴OC•AQ=OA•OB.即
•AQ=1×b.
解得:AQ=4,此时b=17>2符合题意,
∴点Q的坐标是(1,4).
∴综上可知,存在点Q(1,2+
)或Q(1,4),使得△QCO,△QOA和△QAB中的任意两个三角形均相似.
| 1 |
| 4 |
| 1 |
| 4 |
| b |
| 4 |
解得:x=1或b,
∵b是实数且b>2,点A位于点B的左侧,
∴点B的坐标为(b,0),
令x=0,
解得:y=
| b |
| 4 |
∴点C的坐标为(0,
| b |
| 4 |
故答案为:(b,0),(0,
| b |
| 4 |
(2)存在,
假设存在这样的点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形.
设点P的坐标为(x,y),连接OP.
则S四边形PCOB=S△PCO+S△POB=
| 1 |
| 2 |
| b |
| 4 |
| 1 |
| 2 |
∴x+4y=16.
过P作PD⊥x轴,PE⊥y轴,垂足分别为D、E,
∴∠PEO=∠EOD=∠ODP=90°.
∴四边形PEOD是矩形.

∴∠EPD=90°.
∴∠EPC=∠DPB.
∴△PEC≌△PDB,∴PE=PD,即x=y.
由
|
|
由△PEC≌△PDB得EC=DB,即
| 16 |
| 5 |
| b |
| 4 |
| 16 |
| 5 |
解得b=
| 128 |
| 25 |
∴P的坐标为(
| 16 |
| 5 |
| 16 |
| 5 |
(3)假设存在这样的点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似.
∵∠QAB=∠AOQ+∠AQO,
∴∠QAB>∠AOQ,∠QAB>∠AQO.
∴要使△QOA与△QAB相似,只能∠QAO=∠BAQ=90°,即QA⊥x轴.
∵b>2,
∴AB>OA,
∴∠Q0A>∠ABQ.
∴只能∠AOQ=∠AQB.此时∠OQB=90°,
由QA⊥x轴知QA∥y轴.
∴∠COQ=∠OQA.
∴要使△QOA与△OQC相似,只能∠QCO=90°或∠OQC=90°.
(I)当∠OCQ=90°时,△CQO≌△QOA.
∴AQ=CO=
| b |
| 4 |
由AQ2=OA•AB得:(
| b |
| 4 |
解得:b=8±4
| 3 |
∵b>2,

∴b=8+4
| 3 |
∴点Q的坐标是(1,2+
| 3 |
(II)当∠OQC=90°时,△OCQ∽△QOA,
∴
| OQ |
| CO |
| AQ |
| QO |
又OQ2=OA•OB,
∴OC•AQ=OA•OB.即
| b |
| 4 |
解得:AQ=4,此时b=17>2符合题意,
∴点Q的坐标是(1,4).
∴综上可知,存在点Q(1,2+
| 3 |
点评:此题是一道综合题,难度较大,主要考查二次函数的性质,全等三角形的判定和性质,以及相似三角形的判定和性质,还考查等腰三角形的性质及勾股定理,同时还让学生探究存在性问题,对待问题要思考全面,学会分类讨论的思想.

练习册系列答案
相关题目
 (2012•苏州)如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( )
(2012•苏州)如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( ) (cm),其中0≤x≤2.5.
(cm),其中0≤x≤2.5.
 (2012•苏州)如图,已知BD是⊙O的直径,点A、C在⊙O上,
(2012•苏州)如图,已知BD是⊙O的直径,点A、C在⊙O上,